Թեմա՝ Սուրանկյուն, ուղղանկյուն և բութանկյուն եռանկյուններ

Եռանկյան անկյունների գումարի թեորեմի չորրորդ հետևանքի համաձայն՝ անկյուններից կախված գոյություն ունեն եռանկյունների երեք տեսակներ:

Եթե եռանկյան երեք անկյունները սուր են, ապա եռանկյունը կոչվում է սուրանկյուն եռանկյուն:

Եթե եռանկյան անկյուններից մեկը բութ , ապա եռանկյունը կոչվում է բութանկյուն եռանկյուն:

Եթե եռանկյան անկյուններից մեկը ուղիղ է, ապա եռանկյունը կոչվում է ուղղանկյուն եռանկյուն:

Ուղղանկյուն եռանկյան ուղիղ անկյան դիմացի կողմը կոչվում է ներքնաձիգ, իսկ մյուս երկու կողմերը՝ էջեր:

Հարցեր և առաջադրանքներ։

1․Ո՞ր եռանկյունն է կոչվում սուրանկյուն։ GEOGEBRA ծրագրով գծել սուրանկյուն եռանկյուն։

2. Ո՞ր եռանկյունն է կոչվում բութանկյուն։ GEOGEBRA ծրագրով գծել բութանկյուն եռանկյուն։

3. Ո՞ր եռանկյունն է կոչվում ուղղանկյուն։ GEOGEBRA ծրագրով գծել ուղղանկյուն եռանկյուն։

4․ Ինչպե՞ս են կոչվում ուղղանկյուն եռանկյան կողմերը։

5․ Կարո՞ղ է եռանկյունն ունենալ երկու բութ անկյուն: Պատասխանը հիմնավորել։

6․Կարո՞ղ է եռանկյունն ունենալ երկու ուղիղ անկյուն: Պատասխանը հիմնավորել։

7․ Եռանկյունն ունի 32 աստիճանի երկու անկյուն: Տրված եռանկյունը՝

• բութանկյուն է:
• ուղղանկյուն է:
• սուրանկյուն է:

8․ Հայտնի է, որ, MLK-ն եռանկյան անկյուններից ∠MLK=51° է: Նշել MLK եռանկյան տեսակը.

• սուրանկյուն
• բութանկյուն
• հնարավոր չէ պարզել
• ուղղանկյուն

9․ Տրված է NEC եռանկյունը: ∠N=27°, ∠E=99°: Որոշել եռանկյան տեսակը։

10․Հավասարասրուն եռանկյան հիմքին առընթեր անկյուններից մեկի մեծությունը 35° է:

Որոշել եռանկյան գագաթի անկյան մեծությունը և եռանկյան տեսակը։

11․Տրված է KEG եռանկյունը և նրա ∠GKE և ∠GEK անկյունների կիսորդները:

Որոշել կիսորդների կազմած ∠KME անկյունը, եթե ∠GKE=48° և ∠GEK=58°-ի:

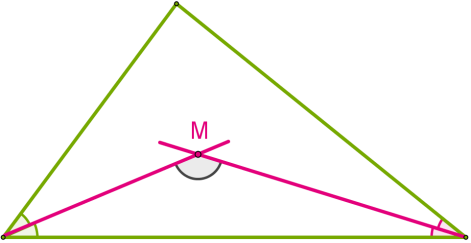
Տրված է KEG եռանկյունը և նրա∡GKE և ∡GEK անկյունների կիսորդները:

Որոշիր կիսորդների կազմած∡KME անկյունը, եթե ∡GKE=48° և ∡GEK=58°-ի:

1. Տրված է ABC եռանկյունը: ∠A=25°, ∠B=98°: Որոշել ∠C անկյան մեծությունը:

98 + 25 = 123

180 – 123 = 57

2. Տրված է ուղղանկյուն եռանկյուն, որի սուր անկյուններից մեկի մեծությունը 68° է: Որոշել այդ եռանկյան մյուս սուր անկյան մեծությունը:  

90 + 68 = 158

180 – 158 = 22

3. Տրված է ADM հավասարասրուն եռանկյան գագաթի ∠D անկյան մեծությունը` ∠D=138°: Որոշել հիմքին առընթեր անկյունների մեծությունները:

180 – 138 = 42

42/2 = 21

4. Հավասարասրուն եռանկյան հիմքին առընթեր անկյուններից մեկի մեծությունը 48° է: Որոշել եռանկյան գագաթի անկյան մեծությունը:

48 * 2 = 96

180 – 96 = 84

5. Որոշել KMN եռանկյան անկյունների մեծությունները, եթե ∠K:∠M:∠N=4:3:5:
4x + 3x + 5x = 180
12x = 180
x = 180/12 = 15
∠K = 4 * 15 = 60, ∠M = 3 * 15 = 45, ∠N = 5 * 15 = 75
6․ Հավասարասրուն եռանկյան արտաքին անկյուններից մեկը 115⁰ է: Գտնել եռանկյան անկյունները:
180 – 115 = 65
65 * 2 = 130
180 – 130 = 50

7․ Գտնել անհայտ անկյունները։

ա)

180 – 150 = 30
70 + 30 = 100
180 – 100 = 80

բ)

A = 70
70 + 64 = 134
180 – 134 = 46

գ)

A = 56
180 – 110 = 70
70 + 56 = 126
180 – 126 = 54

դ)

180 – 120 = 60
180 – 87 = 93
93 + 60 = 153
180 – 153 = 27

ե)

ABK = 40
40 * 2 = 80
BKA = 180 – 80 = 100
BKC = 180 – 100 = 80
KCB = 80
KBC = 180 – 80 * 2 = 20

8․ Որոշել AKM հավասարասրուն եռանկյան անկյունների մեծությունները, եթե հիմքին հանդիպակած K գագաթի անկյան կից անկյունը հավասար է 156°-ի:

180 – 156 = 24

156/2 = 78

9․Գտնել հավասարասրուն եռանկյան հիմքին առընթեր անկյունը, եթե գագաթի անկյունը 12°-ով մեծ է հիմքին առընթեր անկյունից։

x + x + x + 12 = 180

3x = 180 – 12 = 168
x = 168/3 = 56

56 + 12 = 68