Թեմա՝ Առնչություններ եռանկյան կողմերի և անկյունների միջև

Եռանկյան ավելի մեծ կողմի դիմաց ընկած է ավելի մեծ անկյունը:

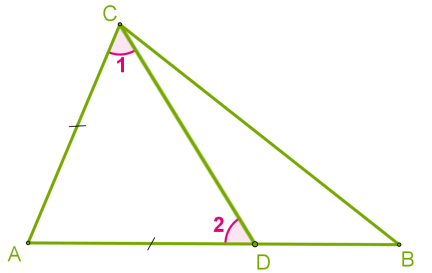
Ապացույց:

Դիցուք ABC եռանկյան մեջ AB կողմն ավելի մեծ է AC կողմից:

Ապացուցենք, որ ∡C>∡B:

Տեղադրենք AB կողմի վրա AC-ին հավասար հատված:

Քանի որ AD<AB, ապա D կետն ընկած է A և B կետերի միջև:

Հետևաբար, 1 անկյունը հանդիսանում է C անկյան մաս, և ուրեմն՝ ∡C>∡1

2 անկյունը BDC եռանկյան արտաքին անկյունն է, ուստի ∡2>∡B

∡1=∡2՝ որպես ADC հավասարասրուն եռանկյան հիմքին առընթեր անկյուններ:

Այսպիսով, ∡C>∡1=∡2>∡B

Այստեղից հետևում է, որ ∡C>∡B

Տեղի ունի նաև հակառակ պնդումը.

Եռանկյան ավելի մեծ անկյան դիմաց ընկած է ավելի մեծ կողմ:

Հետևանքներ.

Հետևանք 1.

Եթե եռանկյան երկու անկյուններ հավասար են, ապա եռանկյունը հավասարասրուն է (հավասարասրուն եռանկյան հայտանիշ):

Հետևանք 2.

Եթե եռանկյան երեք անկյուններ հավասար են, ապա եռանկյունը հավասարակողմ է:

Հետևանք 3.

Ուղղանկյան եռանկյան ներքնաձիգն ավելի մեծ է էջից:

Առաջադրանքներ։

1․GEOGEBRA ծրագրով  գծել ABC բութանկյուն եռանկյուն, նշել եռանկյան ամենամեծ կողմը։

2․GEOGEBRA ծրագրով  գծել ABC  ուղղանկյուն եռանկյուն, որի ուղիղ անկյունը C-ն է, նշել եռանկյան ամենամեծ կողմը։

3․Տրված է CAB եռանկյունը: Նշել  A անկյան հանդիպակաց կողմը:

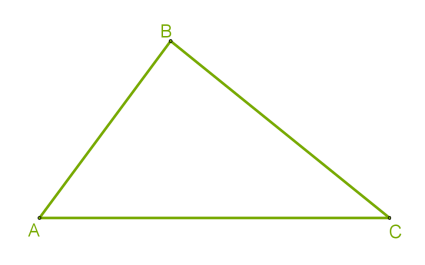
ա) AB բ) CA գ) CB

4․ABC եռանկյան մեջ նշել CAB անկյան հանդիպակաց կողմը:

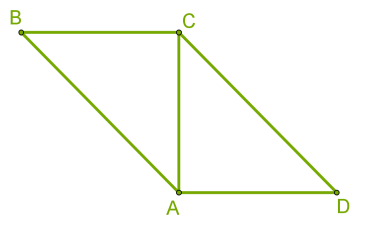
ա) BC բ) CD գ) AB դ) DB ե) DA զ) CA

5․ Ընտրել  նկարում ցուցադրված եռանկյան տեսակը: Հնարավոր է մի քանի ճիշտ պատասխան:

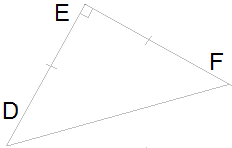
• բութանկյուն
• սուրանկյուն
• հավասարասրուն
• ուղղանկյուն
• ոչ հավասարասրուն
• հավասարակողմ

6․ Հաշվել ACB եռանկյան պարագիծը, եթե AB=AC=BC=12 դմ:

12 * 3 = 36

7․ Հաշվել  ACB եռանկյան պարագիծը, եթե CA=BC=17սմ  և BA=22 սմ․

17 * 2 + 22 = 56

8․ Գտնել  ACB եռանկյան պարագիծը, եթե CA=55 սմ, BC=33սմ և AB=44սմ

55 + 33 + 44 = 132

9․Հաշվել հավասարակողմ եռանկյան կողմը, եթե նրա պարագիծը հավասար է 222 սմ-ի:

222 / 3 = 74

10․Հավասարասրուն եռանկյան պարագիծը հավասար է 60մ-ի, իսկ նրա սրունքը հավասար է 21մ-ի: Հաշվել եռանկյան հիմքը:

60 – 21 * 2 = 18

11․ Եռանկյան պարագիծը հավասար է 50 սմ-ի: Եռանկյան մի կողմը 20 սմ է: Հաշվել եռանկյան մյուս երկու կողմերը, եթե հայտնի է, որ դրանք իրար հավասար են:

(50 – 20) / 2 = 15

12․ Տրված է ΔABC, AC=BC: Եռանկյան հիմքը 12 դմ-ով փոքր է սրունքից: ABC եռանկյան պարագիծը հավասար է 132 դմ-ի: Հաշվել եռանկյան կողմերը:

3x-12=132

3x=144

x = 144/3 = 48

AC=BC = 48

AB = 48 – 12 = 36

13․ Տրված են AKM եռանկյան անկյունների մեծությունները՝ ∠A=62°,∠K=87°,∠M=31°:

Թվարկիր եռանկյան կողմերը՝ ամենափոքրից մինչև ամենամեծը:

AK, KM, AM,

1.Տրված է ABC եռանկյունը: ∠A=34°, ∠B=78°: Որոշել ∠C անկյան մեծությունը:
34 + 78 = 112
180 – 112 = 68

2. Տրված է ուղղանկյուն եռանկյուն, որի սուր անկյուններից մեկի մեծությունը 27° է: Որոշել այդ եռանկյան մյուս սուր անկյան մեծությունը:
27 + 90 = 117
180 – 117 = 63

3․ Որոշել NLM եռանկյան անկյունների մեծությունները և եռանկյան տեսակը, եթե ∠N:∠L:∠M=6:2:4
6x + 2x + 4x = 180
12x = 180
x = 15
∠N = 6 * 15 = 90°
∠L = 2 * 15 = 30°
∠M = 4 * 15 = 60°
Եռանկյունը ուղղանկյուն է:

4․Գտնել եռանկյան անհայտ անկյունը․

ա)

180 – 150 = 30
180 – 110 = 70
70 + 30 = 100
180 – 100 = 80

բ)

60 + 50 = 110
180 – 110 = 70

գ)

180 – 138 = 42
42 + 28 = 70
180 – 70 = 110

5․ Գտնել եռանկյան արտաքին անկյունը։

ա)

65 + 45 = 110

բ)

180 – 110 = 70
70 + 50 = 120

գ)

80 * 2 = 160

6․ Գտնել անհայտ անկյունները․

59 + 90 = 149
180 – 149 = 31
y = 31
90 + 31 = 121
180 – 121 = 59
x = 59

1․Ո՞ր եռանկյունն է կոչվում սուրանկյուն։ GEOGEBRA ծրագրով գծել սուրանկյուն եռանկյուն։

2. Ո՞ր եռանկյունն է կոչվում բութանկյուն։ GEOGEBRA ծրագրով գծել բութանկյուն եռանկյուն։

3. Ո՞ր եռանկյունն է կոչվում ուղղանկյուն։ GEOGEBRA ծրագրով գծել ուղղանկյուն եռանկյուն։

4․ Ինչպե՞ս են կոչվում ուղղանկյուն եռանկյան կողմերը։
Էջ, էջ, ներքնաձիգ

5․ Կարո՞ղ է եռանկյունն ունենալ երկու բութ անկյուն: Պատասխանը հիմնավորել։
Քանի որ բութ անկյունը մեծ է 90^օ, իսկ եռանկյան անկյունների գումարը 180^օ է ապա եռանկյունը չի կարող ունենալ 2 բութ անկյուն։

6․Կարո՞ղ է եռանկյունն ունենալ երկու ուղիղ անկյուն: Պատասխանը հիմնավորել։
Ոչ, որովհետև 2 ուղիղ անկյան գուրամը 180^օ է, իսկ եռանկյունը ունի 3 անկյուն։

7․ Եռանկյունն ունի 32 աստիճանի երկու անկյուն: Տրված եռանկյունը՝

• բութանկյուն է:
• ուղղանկյուն է:
• սուրանկյուն է:

8․ Հայտնի է, որ, MLK-ն եռանկյան անկյուններից ∠MLK=51° է: Նշել MLK եռանկյան տեսակը.

• սուրանկյուն
• բութանկյուն
• հնարավոր չէ պարզել
• ուղղանկյուն

9․ Տրված է NEC եռանկյունը: ∠N=27°, ∠E=99°: Որոշել եռանկյան տեսակը։
բութանկյուն, ∠E > 90^o

10․Հավասարասրուն եռանկյան հիմքին առընթեր անկյուններից մեկի մեծությունը 35° է: Որոշել եռանկյան գագաթի անկյան մեծությունը և եռանկյան տեսակը։

180 – 2 * 35 = 110
բութանկյուն է:

11․Տրված է KEG եռանկյունը և նրա ∠GKE և ∠GEK անկյունների կիսորդները: Որոշել կիսորդների կազմած ∠KME անկյունը, եթե ∠GKE=48° և ∠GEK=58°-ի:

48 : 2 = 24
58 : 2 = 29
180 – (29 + 24) = 127