Թեմա՝ Հիմնական հասկացություններ բազմությունների մասին։
Բազմությունը որևէ առարկաների, իրերի, գաղափարների հավաքածու է, որոնք կոչվում են այդ բազմության տարրեր:
Սովորաբար բազմությունը նշանակում են լատինական այբուբենի մեծատառերով՝ A,B,C,…,իսկ բազմության տարրերը՝ նույն այբուբենի փոքրատառերով՝ a,b,c,…:
Բազմությունը բաղկացած է տարրերից. դա գրում են ձևավոր փակագծերի միջոցով՝ A={a1;a2;…;an}
Եթե a-ն A բազմության տարր է, ապա ասում են՝ «a-ն պատկանում է A-ին» և գրում ∈ պատկանելիության նշանի միջոցով՝ a∈A: ∉ նշանը ցույց է տալիս, որ տարրը չի պատկանում բազմությանը:
Օրինակ՝ −8∉N նշանակում է, որ −8 թիվը չի պատկանում բնական թվերի բազմությանը:
Բազմության տարրերի հերթականությունը կարևոր չէ:
Օրինակ՝ {a,b,c}և{c,b,a} բազմությունները նույն են, կամ հավասար են:
Երկու բազմություններ անվանում են հավասար, եթե նրանք բաղկացած են միևնույն տարրերից:
Ոչ մի տարր չպարունակող բազմությունը անվանում են դատարկ բազմություն և նշանակում են ∅ նշանով:
Վերջավոր թվով տարրերից բաղկացած բազմությունը կոչվում է վերջավոր բազմություն:
Օրինակ՝ մեկ a տարրից բաղկացած A={a} բազմությունը վերջավոր է:
Բնական թվերի N={1,2,3,4,5…} բազմությունը վերջավոր չէ կամ անվերջ է:
Բազմության տարրերից, տարբեր խմբավորումներով, կարելի է կազմել նոր բազմություններ:
Եթե A բազմության ցանկացած տարր հանդիսանում է նաև B բազմության տարր, ապա ասում են, որ A-ն B բազմության ենթաբազմություն է և գրում են՝ A⊂B
Մասնավորապես՝ բազմությունը իր ենթաբազմությունն է՝ A⊂A
Ուշադրություն՝ Չխառնես ∈ և ⊂ նշանները:
Օրինակ՝ այս 3∈{0,1,2,3,4,5} գրառումը ճիշտ է, քանի որ 3 թիվը հանդիսանում է {0,1,2,3,4,5} բազմության տարր: Իսկ 3⊂{0,1,2,3,4,5} գրառումը ճիշտ չէ՝ ձախ մասում թիվ է, իսկ պետք է բազմություն լինի:
A և B բազմությունների միավորում անվանում են այն բազմությունը, որը բաղկացած է բոլոր այն տարրերից, որոնք պատկանում են A և B բազմություններից գոնե մեկին: Միավորումը նշանակում են այսպես՝ A∪B
Բազմությունները հարմար է ներկայացնել շրջանների տեսքով, որոնք անվանում են Էյլերի շրջաններ:

A և B բազմությունների հատում անվանում են այն բազմությունը, որի տարրերը պատկանում են միաժամանակ և՛ A, և՛ B բազմություններին: Հատումը նշանակում են այսպես՝ A∩B:
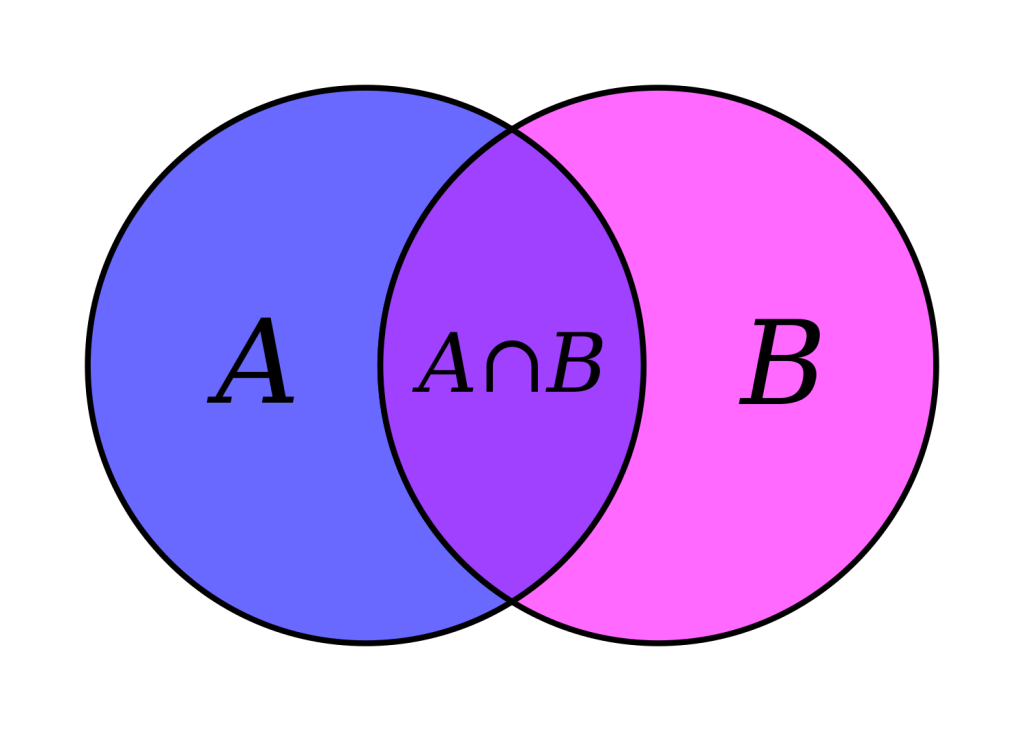
Օրինակ` Գտնենք A և B բազմությունների հատումը , եթե, A={0,1,2,3,4,5,6,7,8,9} և B={2,4,6,8,10}
Ընդգրկենք ընդհանուր տարրերը և բացառենք մնացած տարրերը՝ A∩B={2,4,6,8}
Հարցեր և առաջադրանքներ։
1․ Ի՞նչ է բազմությունը։
Բազմությունը որևէ առարկաների, իրերի, գաղափարների հավաքածու է, որոնք կոչվում են այդ բազմության տարրեր:
2․ Ո՞ր բազմություններն են հավասար։
որենք ունես նույն տարրերը
3․ Բերել վերջավոր և անվերջ բազմությունների օրինակներ։
Օրինակ կենդանիների բազմության վերջավոր։
4․ Ընտրել բազմությունը՝ բառերով տրված նկարագրի հիման վրա: −6-ից մեծ ամբողջ բացասական թվեր: Ընտրել պատասխանի ճիշտ տարբերակը:
ա) {−5,−4,−3,−2,−1} բ) {1,2,3} գ) {−1,−2,−3,−4,−5,−6} դ) {1,2,3,4}
5․ Ընտրել ճիշտ պնդումները.
ա) 0.5∈N բ) 13∈N գ) 12∈N դ) 20∈N ե) 2∈{−3,3} զ) x∉{x+1} է) −3∈N ը) a∈{a} թ) z∈{x,y,z}
6․Այս բազմություններից ո՞րն է վերջավոր: Ընտրել պատասխանի ճիշտ տարբերակը:
- զրոյից փոքր ամբողջ թվեր
- երկուսից փոքր բնական թվեր
- զրոյից մեծ բնական թվեր
- մինուս չորսից մեծ ամբողջ թվեր
7․Տրված են {1,2,3,4,5} և {2,4,6} բազմությունները: Կազմել բերված բազմությունների միավորումն ու հատումը։
A∩B = {2, 4}
A∪B = {1, 2, 3, 4, 5, 6}
8․ Տրված են երկու բազմություններ՝ A={x,2y,z},B={x, y}: Գտնել նրանց միավորումն ու հատումը: ա) A∪B բ) A∩B
A∩B = {x}
A∪B = {x, 2y, z, y}
9․ Տեղի ունի բազմությունների միավորման այս հավասարությունը՝ {x, y}∪{0,4}={x, y}
ա) որոշել x-ը, եթե y-ը բնական թիվ չէ:
x = 4 y = 0
բ) որոշել x-ը, եթե y-ը բնական թիվ է:
x = 0 y = 4
10․Տրված են երկու բազմություններ՝ A={3,5,7}, B={2,4}: Կազմել տրված բազմությունների միավորումն ու հատումը:
A∪B = 2, 3, 4, 5, 7
A∩B = ∅
11․Տրված է երկու բազմություն՝ A և B: A-ն ունի 15 տարր, իսկ B-ն՝ 4: Որոշել A և B բազմությունների միավորման տարրերի թիվը, եթե դրանց հատումն ունի 1 տարր:
A∪B = 15 + 4 – 1 = 18
12․Տրված է երկու բազմություն՝ A և B: A-ն ունի 12 տարր, իսկ B-ն՝ 16: Պարզել A և B բազմությունների հատման տարրերի թիվը, եթե դրանց միավորումն ունի 20 տարր:
A = 12
B = 16
A∪B = 20
20 = 12 + 16 – A∩B
20 – 28 – A∩B
A∩B = 20
13․Տրված է երկու բազմություն՝ A={2,4,6,8,…,20} և B={1,2,3,…,133}: Գտնել դրանց հատումը:
A∩B = A
A∪B = B