Թեմա՝ Ուղիղ համեմատականության ֆունկցիան և նրա գրաֆիկը։

y=kx տեսքի ֆունկցիան, որտեղ k−ն զրոյից տարբեր տրված թիվ է, անվանում են ուղիղ համեմատական կախում: k թիվը կոչվում է ուղիղ համեմատականության գործակից: 

y=kx ֆունկցիան իմաստ ունի ցանկացած x-ի համար: Ունենալով x-ի ցանկացած արժեք՝ բանաձևի օգնությամբ կարելի է հաշվել y-ի համապատասխան արժեքը: Սա նշանակում է, որ y=kx ֆունկցիայի որոշման տիրույթը բոլոր իրական թվերի բազմությունն է: 

Օրինակ: Կառուցենք y=0,5x ֆունկցիայի գրաֆիկը: 

Բանաձևից ստանում ենք, որ՝ եթե x=0, ապա y=0: Սա նշանակում է, որ ուղիղ համեմատականության գրաֆիկը անցնում է կոորդինատների սկզբնակետով;

Եթե x=2, ապա y=1, եթե x=4, ապա y=2, եթե x=6, ապա y=3 և այլն:

Սովորաբար այս արդյունքները ներկայացնում են աղյուսակի տեսքով:

x	0	2	4	6
y	0	1	2	3

x-ը անկախ փոփոխականն է (կամ արգումենտը), y-ը կախյալ փոփոխականն է:

Այսպիսով, գրաֆիկը անցնում է (0;0),(2;1),(4;2),(6;3) կետերով: Քանոնը դնելով այդ կետերի վրա՝ տեսնում ենք, որ դրանք գտնվում են մի ուղղի վրա, որն անցնում է կոորդինատների սկզբնակետով:

Ուղիղ գիծը կառուցելու համար բավական է միացնել նրա վրա գտնվող երկու կետ:

xOy հարթության վրա նշենք վերևի աղյուսակի (0;0) և (4;2) կետերը:

Ստանում ենք հետևյալ ուղիղը, որն էլ հենց հանդիսանում է y=0,5x ֆունկցիայի գրաֆիկը: 

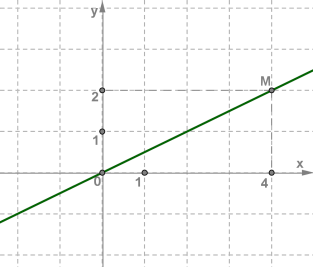
Այնպես, ինչպես կառուցեցինք y=0,5x ֆունկցիայի գրաֆիկը, կարելի է կառուցել y=kx ֆունկցիայի գրաֆիկը ցանկացած k−ի համար և համոզվել, որ՝ y=kx ֆունկցիայի գրաֆիկը ուղիղ գիծ է, որն անցնում է կոորդինատների սկզբնակետով:

y=kx ուղիղ համեմատականության բանաձևից ստանում ենք, որ՝ k=y/x

Հետևաբար, k ուղիղ համեմատականության գործակիցը գտնելու համար բավական է վերցնել ցանկացած կետ նրա գրաֆիկի վրա և գտնել այդ կետի օրդինատի հարաբերությունը աբսցիսին:

Քանի որ y=kx ֆունկցիայի գրաֆիկը (0;0) կետով անցնող ուղիղ գիծ է, ապա ընդհանուր դեպքում այդ ֆունկցիայի գրաֆիկը կառուցելու համար պետք է գտնել ևս մեկ կետ գրաֆիկի վրա: Ուղիղ գիծը, որն անցնում է այդ կետով և (0;0) կետով հենց կլինի պահանջվող գրաֆիկը: Սովորաբար այդ կետի դերում վերցնում են (1;k) կետը (եթե x=1, ապա y=kx բանաձևից ստանում ենք՝ y=k

k գործակցից է կախված անկյունը y=kx ֆունկցիայի գրաֆիկի և x-երի առանցքի դրական ուղղության միջև:

Եթե k>0, ապա անկյունը սուր է (ինչպես վերևի օրինակում), իսկ գրաֆիկը անցնում է I և III քառորդներով:

Եթե k<0, ապա անկյունը բութ է (ինչպես ներքևի նկարում), իսկ գրաֆիկը անցնում է  II և  IV քառորդներով:

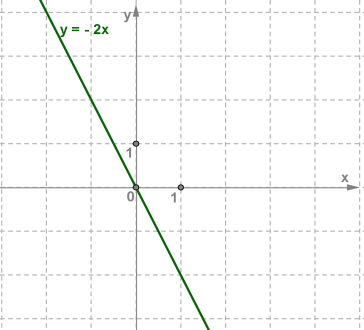
k-ն անվանում են y=kx ուղղի անկյունային գործակից:

Առաջադրանքներ։

1․ Ֆունկցիան ուղիղ համեմատակա՞ն է.
ա) y = x, բ) y = 4x, գ) y = −3x, դ) y = 2x + 1, ե) y = 3x − 2, զ) y = 1− x,
է) y = 0x, ը) y = x ² , թ) y = x ² + x:

2. Ֆունկցիան տրված է y=2x բանաձևով:

ա) Լրացնել աղյուսակը.

x	0	1	-1
y				6	-8

բ) Գտնել y-ը, եթե x-ը հավասար է 3; 5; −3; −4:

գ) Գտնել x-ը, եթե y-ը հավասար է 8; 4; −2; 1:

3․ Որոշել y=kx ֆունկցիայի k գործակիցը, եթե

ա) x = 3, y = 6; բ) x = −2, y = −10;

գ) x = 2, y = −8; դ) x = −1, y = 4:

4․ Կառուցել ֆունկցիայի գրաֆիկը.
ա) y = 2x;    բ) y = −4x;    գ) y = x/2;    դ) y = — 0,25x:

5․ Որոշել y = kx ֆունկցիայի k գործակիցը և լրացնել աղյուսակը. ա)

x	3	1	0
y	9			12	-3

բ)

x			10	6	1
y	0	3	5

գ)

x	2	4	5
y			10	14	-6

6․ Գծել ուղիղ համեմատականության ֆունկցիայի գրաֆիկը, որն անցնում է հետևյալ կետով. ա) (2, 2), բ) (3, −6), գ) (5, 2), դ) (− 2, 1):

7․Ո՞ր քառորդներով է անցնում y=−2x  ֆունկցիայի գրաֆիկը:

ա) II և IV բ) II և III գ) I և III դ) I և IV