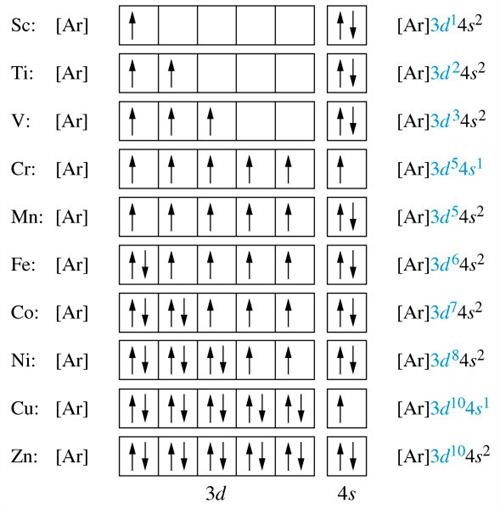
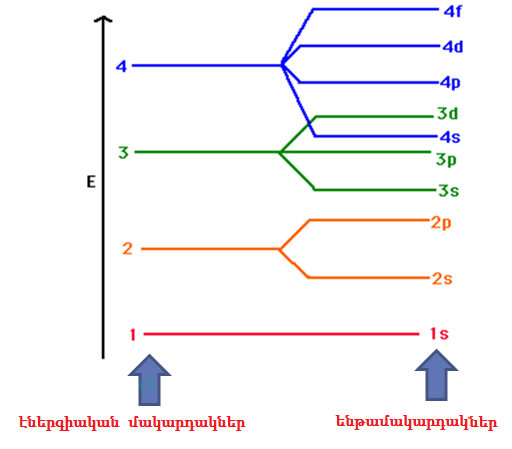
Fill in the blanks with the past continuous form of the verbs given in brackets.
- The children were playing hide and seek in the park. (play)
- They were going to the movies. (go)
- I was reading the book you gave me on my birthday. (read)
- Winnie was stitching her new dress. (stitch)
- The dogs were barking all night. (bark)
- Ron was cleaning his room when he heard the noise. (clean)
- It was getting darker with each passing moment. (get)
- The gardener was watering the lawn. (water)
- The army was going to Ladakh when the enemy attacked them. (go)
- My sister was riding a Royal Enfield yesterday. (ride)
- The students were working on their assignments. (work)
- That boy was dancing in class. (dance)
- The kid was watching television all evening. (watch)
- The girl was listening to rock music. (listen)
- The birds were flying in the sky. (fly)
Ecercise 2 – Change into the past continuous tense
Read the following sentences and change them into the past continuous tense.
1.Raj was drinking coffee.
2.Sweta was singing her favourite song.
3.Siraj was leaving home.
4.My friends were playing on the field.
5.I was going to France.
6.The boy was crying all night.
7.The cat was running in the streets.
8.I was performing at the school function.
9.The parrot was talking back.
10.Tia was visiting her granny.
Put the verbs into the correct form (past progressive).
1.When I phoned my friends, they were playing Monopoly.
2.Yesterday at six I was preparing dinner.
3.The kids were playing in the garden when it suddenly began to rain.
4.I was practicing the guitar when he came home.
5.We were not cycling all day.
6.While Alan was working in his room, his friends were swimming in the pool.
7.I tried to tell them the truth but they were not listening.
8.What were you doing yesterday?
9.Most of the time we were sitting in the park.
10.I was listening to the radio while my sister was watching TV.
11.When I arrived, they were playing cards.
12.We were studying English yesterday at 4:00 pm.