Թեմա՝ Զուգահեռագիծ:

Զուգահեռագիծ կոչվում է այն քառանկյունը, որի հանդիպակաց կողմերը զույգ առ զույգ զուգահեռ են:

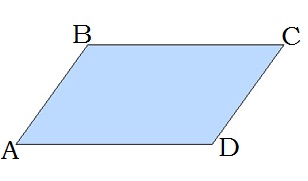
Զուգահեռագծի հատկությունները

1. Զուգահեռագծի հանդիպակաց կողմերը հավասար են՝  AB=DC,BC=AD

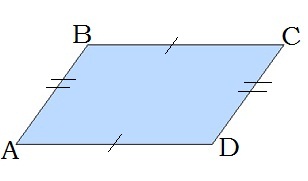
2. Զուգահեռագծի հանդիպակաց անկյունները հավասար են՝  ∠A=∠C, ∠B=∠D

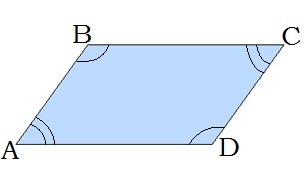
3. Զուգահեռագծի անկյունագծերը հատման կետով կիսվում են՝ BO=OD, AO=OC

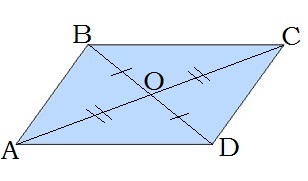
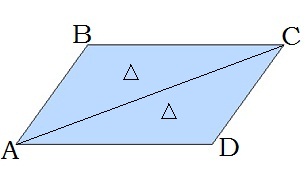
4. Զուգահեռագիծը անկյունագծով բաժանվում է երկու հավասար եռանկյունների՝ ABC և CDA եռանկյունները հավասար են:

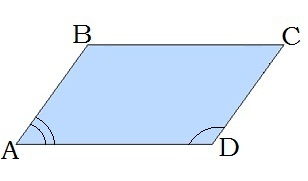
5. Զուգահեռագծի յուրաքանչյուր կողմին առընթեր անկյունների գումարը 180 աստիճան է՝ ∠A+∠D=180°

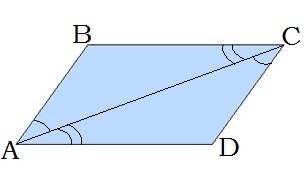
6. Անկյունագծի խաչադիր անկյունները հավասար են՝ ∠BAC=∠ACD,∠BCA=∠CAD

Զուգահեռագծի հայտանիշները

Զուգահեռագծի հայտանիշները թույլ են տալիս պարզելու, թե արդյո՞ք տրված քառանկյունը զուգահեռագիծ է:

1. Եթե քառանկյան երկու կողմերը հավասար են և զուգահեռ, ապա քառանկյունը զուգահեռագիծ է: 

2. Եթե քառանկյան հանդիպակաց կողմերը զույգ առ զույգ հավասար են, ապա քառանկյունը զուգահեռագիծ է: 

3. Եթե քառանկյան անկյունագծերը հատվում և հատման կետով կիսվում են, ապա քառանկյունը զուգահեռագիծ է:  

Օրինակ

1. Կարելի է արդյո՞ք պնդել, որ 4 մ, 4 մ, 6 մ, 6 մ կողմերով քառանկյունը զուգահեռագիծ է:

Պատասխան՝ ոչ, քանի որ տրված չէ, որ հավասար կողմերը հանդիպակաց են:  

2. Զուգահեռագծի հերթականությամբ վերցված կողմերի երկարությունները հավասար են 4 մ, 6 մ, 4 մ, 6 մ : Արդյո՞ք քառանկյունը զուգահեռագիծ է: 

Պատասխան՝ այո, ըստ երկրորդ հայտանիշի:

Առաջադրանքներ

1․ Ո՞ր պատկերն է կոչվում զուգահեռագիծ։

Զուգահեռագիծ կոչվում է այն քառանկյունը, որի հանդիպակաց կողմերը զույգ առ զույգ զուգահեռ են:

2․ Թվարկել զուգահեռագծի հատկությունները

 AB=DC,BC=AD

3․ Տաթևիկը չափեց զուգահեռագծի երկու անկյունները և ստացավ 27 և 164 աստիճանի մեծություններ: Արդյո՞ք նա ճիշտ էր չափել: Պատասխանը հիմնավորել։

4․ Բերված պնդումներից ընտրիր ճիշտ պնդումները զուգահեռագծերի վերաբերյալ:

ա) Զուգահեռագծի անկյունագծերը զուգահեռ են:

բ) Զուգահեռագծի հանդիպակաց կողմերը զուգահեռ են:

գ) Զուգահեռագծի կից կողմերը զուգահեռ չեն:

5․ Զուգահեռագծի պարագիծը 48 սմ է: Գտեք զուգահեռագծի կողմերը, եթե՝

ա) կողմերից մեկը մյուսից մեծ է 3 սմ-ով, բ) կողմերից մեկը երկու անգամ մեծ է մյուսից:

գ) կից կողմերը հարաբերում են ինչպես 1:3-ի:

6․ Զուգահեռագծի անկյուններից մեկը 40 է, գտեք մյուս անկյունները:

7․  Գտեք զուգահեռագծի անկյունները, եթե դրանցից երկուսի գումարը 100է:

8․ Գտեք ABCD զուգահեռագծի անկյունները, եթե՝

ա)∠A=84⁰

բ) ∠A+∠C=142⁰

դ) ∠A=2∠B: