Թեմա՝ Շրջանագծի շոշափող:

Հարցեր և առաջադրանքներ։

1․ Ո՞ր ուղիղն է կոչվում շոշափող:

Եթե ուղիղը շրջանագծի հետ ունի մեկ ընդհանուր կետ, ապա այն կոչվում է շրջանագծի շոշափող:

2. Գրել շրջանագծի շոշափողի հատկությունները:

Եթե միևնույն կետից շրջանագծին տարված են երկու շոշափողներ, ապա

ա) շոշափման կետերի հեռավորությունները տրված կետից հավասար են,

բ) շրջանագծի կենտրոնով և տրված կետով անցնող ուղիղը կիսում է շոշափողների կազմած անկյունը:

3. Տրված է՝  ∠CAO=29°

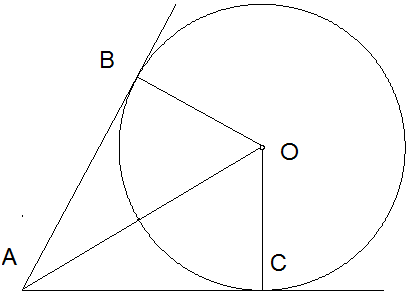
Հաշվել ՝ ∠ABO և ∠COA

90 , 61

4. Տրված է՝ AB=12մ BO=5մ։ Գտնել CA-ն և OC-ն

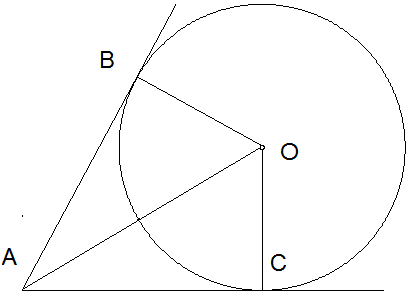
12,5

5. AB ուղիղը B կետում շոշափում է O կենտրոնով և r=2,5 սմ շառավիղով շրջանագիծը: Գտնել ABO եռանկյան անկյունները, եթե AO=5 սմ:

6. Տրված է O կենտրոնով և 3,5 սմ շառավիղով շրջանագիծ: A կետն այնպիսին է, որ AO=7 սմ: A կետով տարված են այդ շրջանագծի երկու շոշափողներ: Գտնել դրանց կազմած անկյունը:

180°−(90°)

7. AB-ն և AC-ն O կենտրոնով շրջանագծին A կետից տարված շոշափողների հատվածներն են : Գտնել BAC անկյունը, եթե AO հատվածի միջնակետը գտնվում է այդ շրջանագծի վրա:

60°

8. Տրված է A անկյանը, որի կողմերը շոշափում են O կենտրոնով և 6,78 սմ շառավղով շրջանագիծը: Հաշվել OA հատվածի երկարությունը, եթե  ∠A=60°:

13.09

Թեմա ՝ Շրջանագծի և ուղղի փոխադարձ դասավորությունը։

Հարցեր և առաջադրանքներ։

Ճիշտ են արդյո՞ք հետևյալ պնդումները:

1. Եթե ուղիղը շրջանագծի շոշափողն է, ապա այն ունի շրջանագծի հետ երկու ընդհանուր կետ:

• Սխալ է: Շոշափողը ուղիղ է, որն ունի շրջանագծի հետ միայն մեկ ընդհանուր կետ՝ շոշափման կետը:

2. Եթե ուղիղը շրջանագծի հետ ունի ընդհանուր կետ, ապա այն հանդիսանում է շրջանագծի հատող:

• Սխալ է: Ուղիղը կարող է ունենալ մեկ ընդհանուր կետ (շոշափող), բայց հատողը պետք է ունենա երկու ընդհանուր կետ:

3. Ուղիղն ու շրջանագիծը կարող են ունենալ միայն երկու ընդհանուր կետ:

Սխալ է: Ուղիղն ու շրջանագիծը կարող են ունենալ 0 (եթե չեն հատվում), 1 (եթե շոշափող են), կամ 2 ընդհանուր կետ (եթե հատող են):

4.Ո՞ր ուղիղն է կոչվում շրջանագծին հատող:

Եթե ուղիղը շրջանագծի հետ ունի երկու ընդհանուր կետեր, ապա այն կոչվում է շրջանագծի հատող:

5.Ո՞ր ուղիղն է կոչվում շրջանագծի շոշափող: 

Եթե ուղիղը շրջանագծի հետ ունի մեկ ընդհանուր կետ, ապա այն կոչվում է շրջանագծի շոշափող:

6.Ո՞ր կետն է կոչվում շրջանագծի և ուղղի շոշափման կետ:

Այն ուղիղը, որը շրջանագծի հետ ունի ընդհանուր կետ

7. Դիցուք՝ d-ն r շառավղով շրջանագծի կենտրոնի հեռավորությունն է p ուղղից: Ինչպե՞ս են միմյանց նկատմամբ դասավորված շրջանագիծը և p ուղիղը, եթե՝

ա) r=18 սմ, d=13 սմ,

հատում է

բ) r=6 սմ, d=5,6 սմ,

հատում է
գ) r=7,2 սմ, d=3,7 դմ,

չի հատում

դ) r=9 սմ, d=1,3 դմ,

չի հատում

ե) r=6 սմ, d=60 մմ:

շոշափում է

8. ABC եռանկյան մեջ AB=10սմ, ∠C=90⁰, ∠B=30⁰: Պահանջվում է տանել A կենտրոնով շրջանագիծ: Ինչպիսի՞ն պետք է լինի այդ շրջանագծի շառավիղը, որպեսզի BC ուղիղը՝

ա) շոշափի շրջանագիծը,

բ) շրջանագծի հետ չունենա ընդհանուր կետ,

գ) շրջանագծի հետ ունենա ընդհանուր կետեր:

9.Տրված է ABCD քառակուսին, որի անկյունագիծը 6 սմ է: Տանել շրջանագիծ, որի կենտրոնը լինի A–ն: Ի՞նչ երկարություն պետք է ունենա շրջանագծի շառավիղը, որպեսզի BD անկյունագիծն ընդգրկող ուղիղը լինի՝ 

ա) շրջանագծի շոշափող
Շրջանագծի շառավիղը պետք է լինի 3սմ։
բ) շրջանագծի հատող:
Շրջանագծի շառավիղը պետք է լինի 3-ից մեծ:

10. AB և CD հատվածները O կենտրոնով շրջանագծի տրամագծեր են: Հաշվեք AOD եռանկյան պարագիծը, եթե հայտնի է, որ CB = 15 սմ, AB = 14 սմ:

16/2=8
P=8+8+13=29

Գիտելիքների ստուգում։

1.  Քանի՞ համաչափության առանցք ունի

    հավասարասրուն  եռանկյունը։

Հավասարասրուն եռանկյունը ունի 1 համաչափության առանցք։

2. Ո՞ր մարմինն է կոչվում   պրիզմա ։ 

Պրիզմա կոչվում է այն տարածական մարմին, որն ունի երկու համանման և զուգահեռ հիմքեր (բազմակողմանիքներ), և այդ հիմքերն իրար միացվում են կողերով, որոնք բոլորն էլ ուղղանկյուն են ըստ այդ հիմքերի։ Պրիզմայի բոլոր կողերը լինում են ուղղանկյուն եւ զուգահեռիմեն։

Օրինակ, եթե հիմքը եռանկյուն է, ապա այդ պրիզման կոչվում է եռանկյան պրիզմա, եթե քառակուսի է՝ քառակուսի պրիզմա, և այլն։

3․ Քանի՞ նիստ, կող, գագաթ ունի

     ուղղանկյումանիստը։

Ուղղանկյունանիստը ունի հետևյալ հատկանիշները՝

• Նիստեր (կողեր)՝ 6 նիստ (4 կողմերի ուղղանկյունները և 2 հիմքի պարսպապատ մակարդակներ)
• Կողեր՝ 12 կող (6 հիմնական կողերից)
• Գագաթներ 8

4․ Խորանարդի անկյունագծի  քառակուսին  

    երկարությունը հավասար է  48 սմ²։

    Գտնել խորանարդի կողի  երկարությունը։

խորանարդի կողի երկարությունը հավասար է 4 սմ։

5․ Գտնել տասնհինգանկյան պրիզմայի

    կողերի,  գագաթների, նիստերի քանակը։

Հակիրճ արդյունք՝

• Կողեր՝ 45
• Գագաթներ՝ 30
• Նիստեր՝ 17

Թեմա՝ Խնդիրների լուծում

1․ Ուղղանկյունանիստի երկարությունը 12 սմ է, լայնությունը երկարությունից 6 սմ ավելի, իսկ բարձրությունը 3 անգամ փոքր լայնությունից: Գտնել ուղղանկյունանիստի լրիվ մակերևույթի մակերեսը: Հուշում ՝ բոլոր նիստերի մակերեսների գումարը հանդիսանում է ուղղանկյունանիստի լրիվ մակերևույթի մակերեսը կամ օգտագործել հետևյալ բանաձևը՝ S=2(ab+bc+ac), որտեղ a, b, c-ն ուղղանկյունանիստի չափումներն են:

S₁=6∙18=108
108∙2=216
S₂=12∙6=72
72∙2=144
S₃=12∙18=216
216∙2=432
216+144+432=792

2․ Խորանարդի նիստերից մեկի պարագիծը 36 սմ է: Գտնել այդ խորանարդի բոլոր կողերի երկարությունների գումարը:

36սմ։4=9սմ
9սմ∙12=108սմ

3․ 60 սմ երկարությամբ մետաղալարը բաժանել են հավասար մասերի և այդ մասերն ընդունելով որպես կողեր՝ պատրաստել են խորանարդ: Գտնել այդ խորանարդի կողի երկարությունը։

60սմ:12=5սմ

4․ Հաշվիր խորանարդի կողի երկարությունը, եթե նրա մակերևույթի ընդհանուր մակերեսը՝ S=2400սմ²:

2400սմ²։6=400
400=20սմ²

5․ Պրիզմայի գագաթների և կողերի թվերի գումարը 40 է: Քանի՞ կող, նիստ և գագաթ ունի այդ պրիզման։

3n+2n=5n
40/5=8
n=8

Կող — 24
Նիստ — 16
Գագաթ — 10

6․ Բուրգի նիստերի և կողերի թվերի գումարը 31 է: Քանի՞ կող, նիստ և գագաթ ունի այդ բուրգը։

31-1=30
x+2x=30
3x=30
x=10
2x=20 (կող)
x+1=11 (նիստ և գագաթ)

7․ Ընտրիր շրջանագծի լարը:

Նշված պատկերի մեջ լարեր են՝ NK,KL,MN:

8․ Գտիր շրջանագծի տրամագիծը, եթե նրա շառավիղը 18,6 սմ է:

18,6×2=37,2սմ

9․ Տրված են շրջանագիծ և մի քանի հատվածներ: Որո՞նք են դրանցից հանդիսանում շառավիղներ, լարեր և տրամագծեր:

Շառավիղ՝ AB, AD, AC,AE,AN.
Տրամագիծ՝ NB, DC.
Լար ՝ FC,NB,DC.

Թեմա՝ Շրջանագիծ

Հարցեր և առաջադրանքներ:

1․ Ո՞ր պատկերն է կոչվում շրջանագիծ:

Շրջանագիծ կոչվում է երկրաչափական այն պատկերը, որը կազմված է հարթության բոլոր այն կետերից, որոնք գտնվում են տրված կետից տրված հեռավորության վրա:   

2. Ի՞նչ է շրջանագծի շառավիղ, տրամագիծը, լարն ու աղեղը:

Շառավիղը հատված է, որը միացնում է շրջանագծի կենտրոնը շրջանագծի ցանկացած կետի հետ: Սահմանումից հետևում է, որ կարելի է տանել անվերջ թվով շառավիղներ, և դրանք բոլորը կունենան միևնույն երկարությունը:

Այն հատվածը, որը միացնում է շրջանագծի երկու կետեր և անցնում է նրա կենտրոնով, անվանում են տրամագիծ։ Շրջանագծի կենտրոնը տրամագիծը բաժանում է երկու շառավղի։

Շրջանագծի երկու կետեր միացնող հատվածը կոչվում է լար:

Շրջանագծի ցանկացած երկու կետեր շրջանագիծը տրոհում են երկու մասի, որոնցից յուրաքանչյուրը կոչվում է շրջանագծի աղեղ:

3․ GEOGEBRA ծրագրով գծել շրջանագիծ և տանել նրա շառավիղը, տրամագիծը և լարը:

4․ Գրել լարի միջնակետով անցնող շառավղի հատկությունները:

1․ Լարի միջնակետով անցնող շառավիղը ուղղահայաց է այդ լարին։

2․ Լարը հատող և նրան ուղղահայաց շառավիղն անցնում է այդ լարի միջնակետով։

5․ Թվարկել   շրջանագծի բոլոր  տրամագծերը,   շառավիղները և  լարերը:

AO,CO,OK,BO,OF-շառավիղ

AB,BC,CD,DE,EF,FK,KL,AL-աղեղ

DF,LE,BF,BL,CK-լար

CK,BF-տրամագիծ

6․ Թվարկել ստացված աղեղները:

ACM,CMP,MPK,PKA

7․ Քանի՞ անգամ է շրջանագծի տրամագիծը մեծ նրա շառավղից։

Մեծ է 2 անգամ։

8․ Ուղիղը հատում է շրջանագիծը A և B կետերում։ Ի՞նչ կետերով պիտի անցնի այդ ուղիղը, որպեսզի AB հատվածն ունենա հնարավոր ամենամեծ երկարությունը։

Այն պետք է լինի տրամագիծը, անցնի կենտրոնով։

9․ Հաշվել CA -ն, եթե CD=8 սմ և ∠AOD=120°։

CA=8սմ:2=4սմ

10․ Տրված է՝ MN=7սմ,  ∠ONM=60°։Գտնել KN-ը։

KN=7սմx2=14սմ

11․ AB հատվածը O կենտրոնով շրջանագծի տրամագիծն է, իսկ AC-ն և BC -ն այդ շրջանագծի հավասար լարեր են։ Գտնել AOC անկյունը։

∠AOC=90°

Թեմա՝ Բուրգ

1.Ո՞ր մարմինն է կոչվում  բուրգ։

Բուրգն  այն  բազմանիստն  է, որի  նիստերից  մեկը  բազմանկյուն  է, իսկ  մյուս  բոլոր նիստերն  ընդհանուր  գագաթով  եռանկյուններ  են:

2.GEOGEBRA ծրագրով գծիր  բուրգ։

3.Ո՞ր նիստերն են կոչվում հիմքեր, կողմնային նիստեր:

Բազմանկյունը  կոչվում  է  բուրգի  հիմք, եռանկյունները՝  կողմնային  նիստեր։

4․Գտեք վեցանկյան բուրգի կողերի, գագաթների, նիստերի քանակը, GEOGEBRA     ծրագրով գծեք վեցանկյուն բուրգ:

3 կող, 5 նիստ, 5 գագաթ

5․Կարո՞ղ է բուրգի կողերի թիվը լինել՝

ա) 13-ոչ, քանի որ 13-ը չի բաժանվում 2-ի

բ) 16- ոչ, քանի որ 16-ը չի բաժանվում 2-ի

գ) 19-ոչ, քանի որ 19-ը չի բաժանվում 2-ի

6․Կարո՞ղ է լինել այնպիսի բուրգ, որն ունի ՝

ա) 9 նիստ/9-1=8,կարող է

բ)  9 կող/9/2=4,5,չի կարող

7․ Ինչպե՞ս է կոչվում այն բուրգը, եթե այն ունի

ա) 13 նիստ

n+1=13
n=12
տասներկուանկյուն բուրգ

բ) 10 գագաթ

10-1=9
իննանկյուն բուրգ

գ) 12 կող

12/2=6
Վեցանկյուն բուրգ

8․Քառանկյուն բուրգի հիմքը 64 սմ պարագծով քառակուսի է, իսկ կողմնային նիստերը հավասարակողմ եռանկյուններ են։ Գտեք բուրգի կողմնային կողերը։

64սմ/4=16սմ

Թեմա՝  Պրիզմա (հատվածակողմ)

Հարցեր և առաջադրանքներ։

1.Որ մարմինն է կոչվում պրիզմա:

Պրիզմա կոչվում է այն բազմանիստը, որի երկու նիստերը զուգահեռ հարթություններում ընկած հավասար բազմանկյուններ են, իսկ մնացած նիստերը ուղղանկյուններ են:

2.GEOGEBRA ծրագրով գծիր պրիզմա:

3.Որ նիստերն են կոչվում հիմքեր, կողմնային նիստեր:

Զուգահեռ հարթություններում գտնվող հավասար նիստերը կոչվում են պրիզմայի հիմքեր, իսկ մնացած նիստերը՝ կողմնային նիստեր:

4.Որ պրիզման է կոչվում ուղիղ պրիզմա։

Եթե պրիզմայի կողմնային կողերը ուղղահայաց են հիմքերին, ապա այն կոչվում է ուղիղ պրիզմա: 

5.GEOGEBRA ծրագրով գծիր ուղիղ պրիզմա:

6.Որ պրիզման է կոչվում թեք պրիզմա։

Իսկ երբ կողմնային կողերը ուղղահայաց չեն հիմքերին, պրիզման կոչվում է թեք:

7․GEOGEBRA ծրագրով գծիր թեք պրիզմա:

8․Գտեք վեցանկյան պրիզմայի կողերի, գագaթների, նիստերի քանակը,GEOGEBRA ծրագրով գծեք վեցանկյան պրիզմա:

Ընդհանուր կողերի քանակը՝ 12+6=18

Երկու հիմքեր միասին ունեն 6+6=12

Ընդհանուր նիստերի քանակը՝ 2+6=8

9․Կարող է պրիզմայի կողերի թիվը լինել՝

ա) 13 բ) 14 գ) 18։ Պատասխանը հիմնավորել։

18 քանի որ բաժանվում է 3-ի

10․Կարող է պրիզմայի նիստերի թիվը լինել՝

ա) 13 բ)14 գ) 18։ Պատասխանը հիմնավորել։

11․ Ինչ բազմանկյուն է պրիզմայի հիմքը, եթե պրիզման ունի ՝

ա) 15 կող բ)11 նիստ գ) 10 գագաթ։

15 կող – 5-անկյուն հիմք,

11 նիստ – 9-անկյուն հիմք,

10 գագաթ – 5-անկյուն հիմք։