Թեմա՝ Ներգծյալ շրջանագիծ

Եթե բազմանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ բազմանկյան ներգծյալ շրջանագիծ:

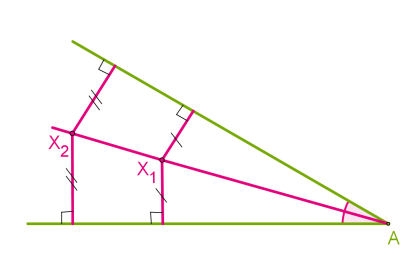
Ներգծված շրջանագծի կենտրոնը պետք է հավասարահեռ լինի բազմանկյան կողմերից, այսինքն լինի կիսորդների հատման կետում:

Եթե քառանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ քառանկյան ներգծյալ շրջանագիծ:

Ոչ բոլոր քառանկյուններն ունեն ներգծյալ շրջանագիծ, քանի որ՝ չորս անկյունների կիսորդները կարող են նույն կետում չհատվել: 

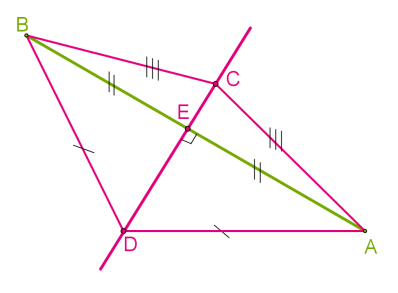
Եթե քառանկյանը ներգծվել է շրջանագիծ, ապա քառանկյան հանդիպակաց կողմերի գումարները հավասար են՝  a+c=b+d:

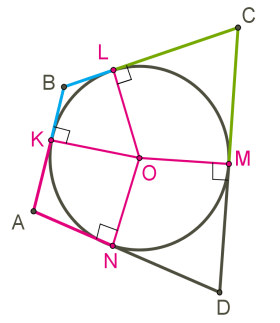
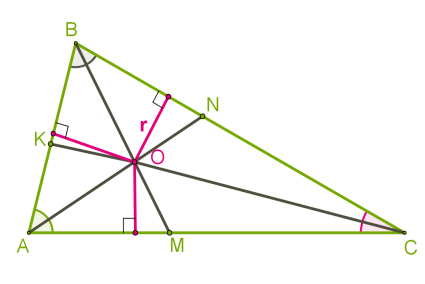
Քառանկյան յուրաքանչյուր կողմ ներկայացնենք երկու հատվածների գումարի տեսքով՝ AB=AK+KB, BC=BL+LC, CD=CM+MD, և AD=DN+NA: Քանի որ, նույն կետից շրջանագծին տարված շոշափողների հատվածները հավասար են, ապա՝ AB+CD=BC+AD:

Այս հատկությունը կարելի է օգտագործել, որպես հայտանիշ, որի միջոցով կարելի է պարզել, թե ո՞ր քառանկյուններն ունեն ներգծյալ շրջանագիծ:

Փորձենք ուղղանկյանը ներգծել շրջանագիծ։Քանի որ ուղղանկյան հանդիպակաց կողմերի գումարը հավասար չէ,ապա չենք կարող ներգծել շրջանագիծ։

Եթե քառանկյան հանդիպակաց կողմերի գումարները հավասար են, ապա այդ քառանկյունն ունի ներգծյալ շրջանագիծ:

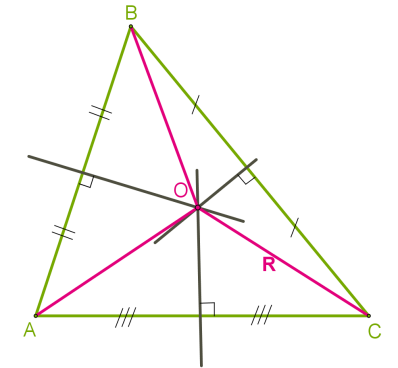
Քանի որ եռանկյան անկյունների կիսորդները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի ներգծյալ շրջանագիծ:

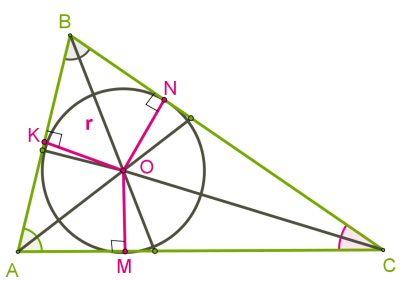
Քանի որ, ցանկացած եռանկյան անկյունների կիսորդները հատվում են եռանկյան ներսում, ապա ներգծյալ շրջանագծի կենտրոնը միշտ գտնվում է եռանկյան ներսում:

Հարցեր և առաջադրանքներ

1․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  ներգծյալ։

Եթե բազմանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ բազմանկյան ներգծյալ շրջանագիծ:

 2․ Քանի՞  շրջանագիծ  կարելի  է  ներգծել  տրված  եռանկյանը:

1 շրջանագիծ

3․GEOGEBRA ծրագրով գծիր եռանկյուն, ներգծիր եռանկյանը շրջանագիծ, նկարը ցույց տուր։

4․Շրջանագծին արտագծած հավասարասրուն սեղանի հիմքերը հավասար են 4 սմ և 9 սմ։ Գտնել սեղանի պարագիծը։

26սմ

5․Ներգծյալ շրջանագծի շոշափման կետում հավասարասրուն եռանկյան սրունքը տրոհվում է 3 սմ և 4 սմ երկարությամբ հատվածների՝ հաշված հիմքից: Գտե՛ք այդ եռանկյան պարագիծը:

34սմ

6․ Գտե՛ք 6 սմ և 8 սմ էջերով և 10սմ ներքնաձիգով ուղղանկյուն եռանկյանը ներգծած շրջանագծի շառավիղը:

2սմ

7․ Ուղղանկյուն եռանկյան ներքնաձիգը 13սմ է, իսկ էջերի գումարը՝ 17սմ: Գտե՛ք եռանկյան ներգծյալ շրջանագծի շառավիղը:

2սմ

8․ Ուղղանկյուն եռանկյան ներքնաձիգը 15 սմ է, իսկ պարագիծը՝ 36սմ: Գտե՛ք այդ եռանկյան ներգծյալ շրջանագծի շառավիղը:

3սմ

Թեմա՝ Եռանկյան նշանավոր կետերը

Թեորեմ 1: Անկյան կիսորդի ցանկացած կետ հավասարահեռ է անկյան կողմերից:

Թեորեմ 2 (հակադարձ): Եթե անկյան մեջ ընկած կետը հավասարահեռ է անկյան կողմերից, ապա այն ընկած է անկյան կիսորդի վրա: 

Թեորեմ 3: Հատվածի միջնուղղահայացի ցանկացած կետ հավասարահեռ է հատվածի ծայրակետերից:

Թեորեմ 4 (հակադարձ): Եթե կետը հավասարահեռ է հատվածի ծայրակետերից, ապա այն ընկած է հատվածի միջնուղղահայացի վրա:

Եռանկյան առաջին նշանավոր կետը՝ կիսորդների հատման կետը

Թեորեմ 5: Եռանկյան անկյունների կիսորդները հատվում են միևնույն կետում:

AN -ը և BM -ը կիսորդներ են, O -ն նրանց հատման կետն է: Այս կետը եռանկյան ներգծյալ շրջանագծի կենտրոնն է և միշտ ընկած է եռանկյան մեջ:

Եռանկյան երկրորդ նշանավոր կետը՝ կողմերի միջնուղղահայացների հատման կետը

Թեորեմ 6: Եռանկյան կողմերի միջնուղղահայացները հատվում են միևնույն կետում:

Դիցուք O կետը AB և BC կողմերի միջնուղղահայացների հատման կետն է: Քանի որ այն հավասարահեռ է A, B և B, C կետերից, ապա, ըստ Թեորեմ 4-ի, այն ընկած է նաև AC կողմի միջնուղղահայացի վրա:

Այս կետը եռանկյան արտագծյալ շրջանագծի կենտրոննէ: Եթե եռանկյունը սուրանկյուն է, ապա կետը ընկած է եռանկյան մեջ, եթե եռանկյունը բութանկյուն է, ապա այն ընկած է եռանկյունից դուրս և, եթե եռանկյունը ուղղանկյուն է, ապա այն ընկած է ներքնաձիգի վրա:

Եռանկյան երրորդ նշանավոր կետը՝ միջնագծերի հատման կետը

Թեորեմ 7: Եռանկյան միջնագծերը հատվում են միևնույն կետում, որը յուրաքանչյուր միջնագիծը բաժանում է 2 : 1 հարաբերությամբ հատվածների՝ հաշված գագաթից:

Միջնակետերի հատման կետն անվանում են եռանկյան ծանրության կենտրոն:

Եռանկյան չորրորդ նշանավոր կետը՝ բարձրությունների հատման կետը

Թեորեմ 8: Եռանկյան բարձրությունները (կամ նրանց շարունակությունները) հատվում են միևնույն կետում:

Բարձրությունների հատման կետն անվանում են եռանկյան օրտոկենտրոն:

Հարցեր և առաջադրանքներ

1․ Գրել չորս նշանավոր կետերը։

• ներգծյալ շրջանագծի կենտրոն
•  արտագծյալ շրջանագծի կենտրոն
• ծանրության կենտրոն
• եռանկյան օրտոկենտրոն

2․ Լուծել խնդիրը

3․ Լուծել խնդիրը

AO=10 սմ

4․ Լուծել խնդիրը

ա)8,5։2=4,25
AD=4,25 սմ
CD=4,25 սմ

բ)3,2×2=6,4
AD=6,4 սմ
CD=6,4 սմ