Պարապմունք 35

Թեմա՝ Կանոնավոր բազմանկյան ներգծյալ և արտագծյալ շրջանագծերը։

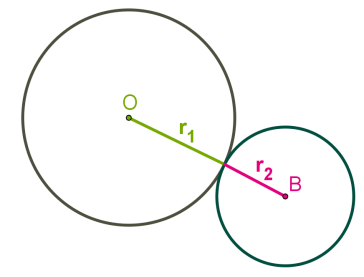
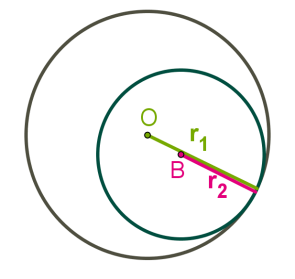
Ցանկացած կանոնավոր բազմանկյանը կարելի է ներգծել և արտագծել շրջանագծեր: Երկու շրջանագծերի կենտրոնները համընկնում են և կոչվում են կանոնավոր բազմանկյան կենտրոն:

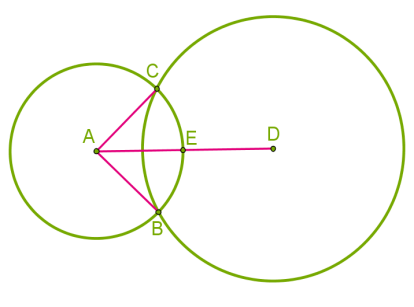
Ներգծյալ շրջանագիծը շոշափում է բազմանկյան բոլոր կողմերը նրանց միջնակետերում։

Արտագծյալ շրջանագիծը անցնում է բազմանկյան բոլոր գագաթներով:

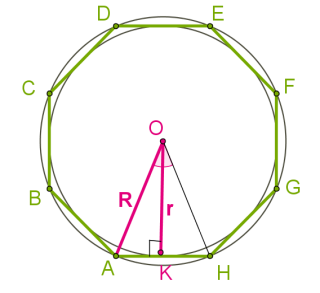
∡AOH=360°/n;∡AOK=360°/2n=180°/n

Հարցեր և առաջադրանքներ։

1․ Ո՞ր բազմանկյունն է կոչվում կանոնավոր։ Բերել օրինակներ

2. GEOGEBRA ծրագրով գծել կանոնավոր եռանկյանը ներգծյալ և արտագծյալ շրջանագծեր։

3․GEOGEBRA ծրագրով գծել կանոնավոր քառանկյանը ներգծյալ և արտագծյալ շրջանագծեր։

4․Ճշմարի՞տ է արդյոք հետևյալ պնդումը․

ա) յուրաքանչյուր կանոնավոր բազմանկյուն ուռուցիկ բազմանկյուն է,

Այո

բ) ցանկացած ուռուցիկ բազմանկյուն կանոնավոր բազմանկյուն է։

Ոչ

5․Հետևյալ պնդումներից որո՞նք են ճշմարիտ․

ա) բազմանկյունը կանոնավոր է, եթե այն ուռուցիկ է, և նրա բոլոր կողմերը հավասար են,

Այո

բ) եռանկյունը կանոնավոր է, եթե նրա բոլոր անկյունները հավասար են,

Այո

գ) հավասար կողմերով յուրաքանչյուր քառանկյուն կանոնավոր քառանկլյուն է։ Պատասխանները հինմավորել։

Այո

6․ Տրված է 13,4 դմ կողմով EFGH քառակուսին:

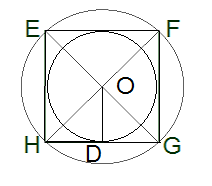
ա) Հաշվիր քառակուսուն ներգծված շրջանագծի շառավիղը:

13.4մ / 2 = 6.7դմ

բ) Հաշվիր քառակուսու մակերեսը:

13.4դմ * 13.4դմ = 179.56դմ^2

7․Տրված է հավասարակողմ եռանկյուն, BO=16սմ:

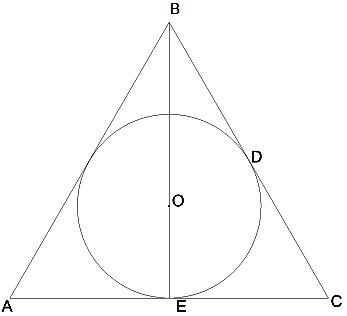
ա) Գտնել ներգծյալ շրջանագծի շառավիղը:

8սմ

բ)Գտնել հետևյալ հատվածների երկարությունները:

OE, BE, AD։

OE = 8սմ
BE = 8սմ
AD = 8սմ

Պարապմունք 34

Թեմա՝ Կանոնավոր բազմանկյուն:

Կանոնավոր բազմանկյուն է կոչվում այն ուռուցիկ բազմանկյունը, որի բոլոր անկյունները և բոլոր կողմերը հավասար են։

Կանոնավոր բազնանկյունների օրինակներ են հավասարակողմ եռանկյունը և քառակուսին։

Նկարում բերված են կանոնավոր բազմանկյունների օրինակներ՝ եռանկյուն (հավասարակողմ), քառանկյուն (քառակուսի), հնգանկյուն, վեցանկյուն:

Արտածենք կանոնավոր n-անկյան α_n անկյունը հաշվելու բանաձևը։ Այդպիսի n-անկյուն բազմանկյան բոլոր անկյունների գումարը հավասար է (n-2) x 180^o։ Քանի որ նրա բոլոր անկյունները հավասար են, ուստի՝

α_n= ${\frac {n-2}{n}}$ x 180°

Հարցեր և առաջադրանքներ:

1․Ո՞ր բազմանկյունն է կոչվում կանոնավոր:

2.Գրել կանոնավոր բազմանկյան անկյան հաշվման բանաձևը:
α_n= (n-2)/n * 180°

3. GEOGEBRA ծրագրով գծել կանոնավոր բազմանկյուններ:

4. Գծագրից գտնել ուռուցիկ բազմանկյունները և նշել նրանց համարները:

1; 6; 9; 10

5. Գտնել կանոնավորn-անկյան անկյունները, եթե՝

ա) n=3
բ) n=5
գ) n=6
դ) n=10
ե) n=18

6. Որոշել կանոնավոր 15 -անկյան ներքին և արտաքին անկյունները:

7. Քանի՞ կողմ ունի կանոնավոր բազմանկյունը, եթե նրա յուրաքանչյուր անկյունը հավասար է` ա) 150^o բ) 135^o գ) 90^o դ) 60^o ե)30^o

8. Քանի՞ կողմ ունի կանոնավոր բազմանկյունը, եթե նրա արտաքին անկյուններից յուրաքանչյուրը հավասար է՝ ա) 40^o բ) 36^o գ) 30^o դ) 24^o

9. Որոշել կանոնավոր բազմանկյան կողմերի թիվը կամ եզրակացրու, որ այդպիսի բազմանկյուն գոյություն չունի, եթե տրված է բոլոր ներքին անկյունների գումարը:

ա) Եթե անկյունների գումարը 2050 աստիճան է, ապա բազմանկյունը գոյություն ….., կողմերի թիվը` …..:

բ) Եթե անկյունների գումարը 1980 աստիճան է, ապա բազմանկյունը գոյություն ……, կողմերի թիվը` …..:

Պարապմունք 33

Թեմա՝ Երկու շրջանագծերի փոխադարձ դասավորությունը։

Հարթության մեջ երկու շրջանագծերի փոխադարձ դասավորությունը կախված է՝

նրանց կենտրոնների դասավորությունից,
նրանց շառավիղների երկարություններից:

Հնարավոր է երեք դեպք:

1) Երկու շրջանագծերը հատվում են՝ ունեն երկու ընդհանուր կետ:

2) Երկու շրջանագծերը շոշափում են՝ ունեն մեկ ընդհանուր կետ:

3) Երկու շրջանագծերը ընդհանուր կետեր չունեն:

Դիտարկենք հնարավոր դեպքերը:

1) Երկու շրջանագծերը հատվում են. ունեն երկու ընդհանուր կետ:

Այս դեպքում կենտրոնների հեռավորությունը փոքր է շառավիղների գումարից:

2) Երկու շրջանագծերը շոշափում են. ունեն մեկ ընդհանուր կետ:

Այս դեպքում հնարավոր են հետևյալ դեպքերը՝

արտաքին շոշափում,
ներքին շոշափում:

Արտաքին շոշափման ժամանակ կենտրոնների հեռավորությունը հավասար է շառավիղների գումարին:

Ներքին շոշափման ժամանակ կենտրոնների հեռավորությունը հավասար է շառավիղների տարբերությանը:

3) Երկու շրջանագծերը ընդհանուր կետեր չունեն:

Այս դեպքում ևս հնարավոր է երկու դեպք:

Երկու շրջանագծերով սահմանափակված շրջանները չեն հատվում:
Փոքր շառավղով շրջանը ընկած է մեծ շառավղով շրջանի մեջ:

Առաջին տարբերակում կենտրոնների հեռավորությունը մեծ է շառավիղների գումարից:

Երկրորդ տարբերակում կենտրոնների հեռավորությունը փոքր է շառավիղների տարբերությունից:

Հարցեր և առաջադրանքներ։

1․Ինչպիսի՞ հնարավոր դասավորվածություն կարող են ունենալ տրված շրջանագծերը եթե նրանց կենտրոնների միջև հեռավորությունը հավասար է 20սմ, իսկ շառավիղները համապատասխանաբար հավասար են՝ ա) 15 սմ և 10 սմ բ) 10 սմ և 10 սմ գ) 5սմ և 7 սմ: GEOGEBRA ծրագրով գծել ստացված պատկերները։

Հատվող