Թեմա՝ Արտագծյալ շրջանագիծ:

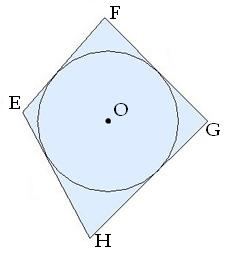
Եթե բազմանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:

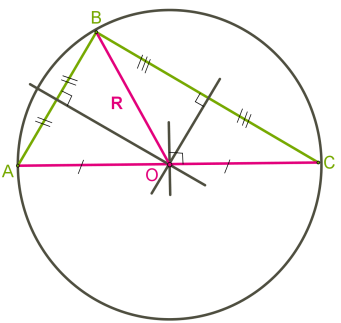
Շրջանագծի կենտրոնը հավասարահեռ է բազմանկյան բոլոր գագաթներից, հետևաբար այն գտնվում է բազմանկյան կողմերի միջնուղղահայացների հատման կետում:

Ոչ բոլոր բազմանկյուններն ունեն արտագծյալ շրջանագիծ՝ հաճախ բազմանկյան համար գոյություն չի ունենում այնպիսի շրջանագիծ, որը կանցնի բազմանկյան բոլոր գագաթներով:  

Եթե քառանկյանը կարելի է շրջանագիծ արտագծել, ապա տեղի ունի հետևյալ հատկությունը՝ Ցանկացած ներգծյալ քառանկյան հանդիպակաց անկյունների գումարը 180⁰ է:

Հետևյալ հատկության միջոցով կարելի է պարզել, թե ո՞ր քառանկյուններն ունեն արտագծյալ շրջանագիծ:

Եթե քառանկյան հանդիպակաց անկյունների գումարը 180° է, ապա նրան կարելի է արտագծել շրջանագիծ:

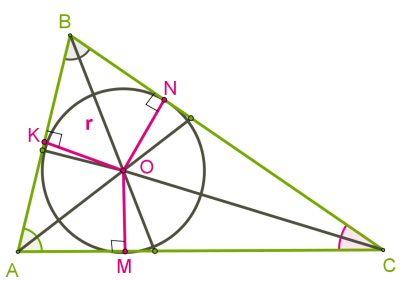
Ի տարբերություն քառանկյունների, բոլոր տեսակի եռանկյուններին հնարավոր արտագծել շրջանագիծ:

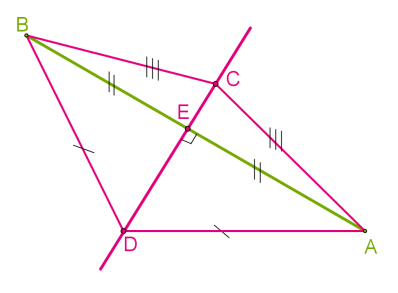
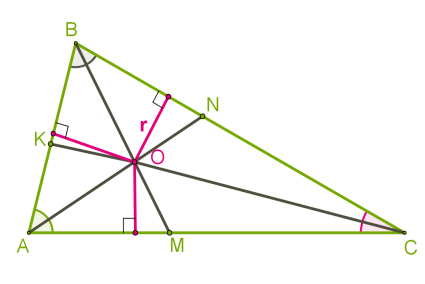
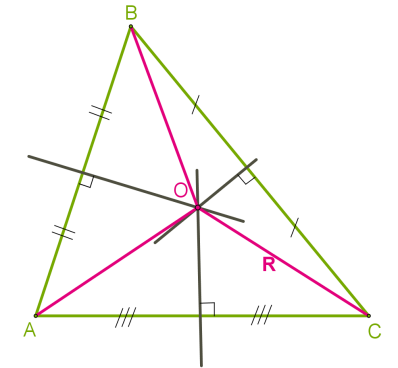
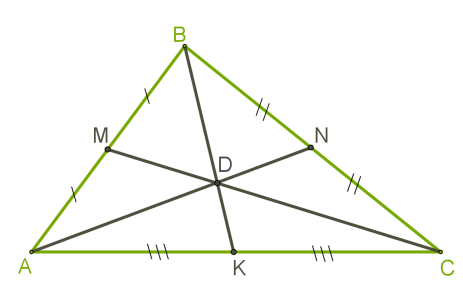
Քանի որ եռանկյան կողմերի միջնուղղահայացները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի արտագծյալ շրջանագիծ: 

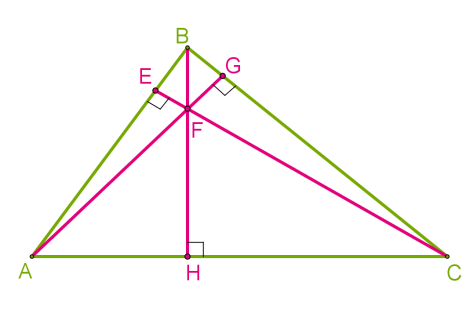
Սուրանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներսում (տես ներքևի նկարը):

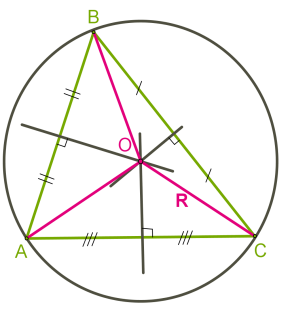
Ուղղանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներքնաձիգի վրա (տես ներքևի նկարը): 

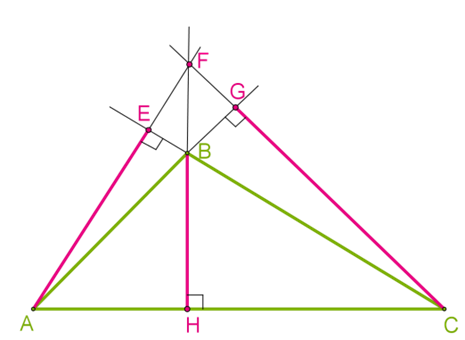
Բութանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյունից դուրս (տես ներքևի նկարը):

Հարցեր և առաջադրանքներ։

1․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  արտագծյալ:    

Եթե բազմանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:

2․ Քանի՞  շրջանագիծ  կարելի  է  արտագծել  տրված  եռանկյանը:

2

3․ Հնարավո՞ր  է  արդյոք  ցանկացած  քառանկյան  արտագծել  շրջանագիծ: 

Ոչ

4․ Ի՞նչ  հատկություն  ունի  շրջանագծին  ներգծված  քառանկյունը:

Պտտվող անկյան հատկություն, պտտվող քառանկյան հատկություն, պտտվող անկյունների հավասարություն։

5․Սեղանին արտագծված է շրջանագիծ: Հաշվիր սեղանի մյուս անկյունները, եթե անկյուններից մեկը՝ F=10° է:

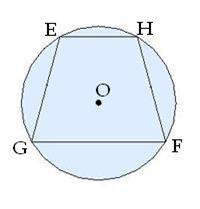
F= G = 10
E=H=170

6․ Գտնել B և D անկյունները։

B = 180-85 = 95
D = 180-117 = 63

7․ O կենտրոնով շրջանագծին ներգծված է ZXY եռանկյունն այնպես, որ ZX-ը  տրամագիծ է։ ZY աղեղի աստիճանային չափը հավասար է 104⁰ -ի։ Գտնել ZXY եռանկյան անկյունները։

X = 104 / 2 = 52
Y = 90
Z = 90 – 52 = 38

8․ Օգտվելով գծագրից, գտնել ∠ B-ը։

B = 90-46 = 44

9․ Գտնել ∠ R-ը և ∠B-ն։

B = 180-92=88
E = 180-74 = 106

10․ ABC եռանկյանը արտագծված է շրջանագիծ։ Գտնել այդ շրջանագծի շառավիղը, եթե AC=24 սմ, ∠A=60⁰, ∠B=30⁰:

սմ, ∠A=60⁰, ∠B=30⁰:
R = 48/2 = 24

11. Արդյոք կարելի՞ է տրված ABCD քառանկյանը արտագծել շրջանագիծ, եթե ա)∠A=64⁰, ∠ B=95⁰, ∠C=106⁰բ) ∠A=72⁰, ∠B=69⁰, ∠D=111⁰ գ) ∠A=90⁰, ∠C=90⁰, ∠D=80⁰:

A+C = 170 ոչ
D+B = 182 այո
A+C = 180 այո

1.Ո՞ր մեծություննէ կոչվում էներգիա

Էներգիան ֆիզիկական մեծություն է, որը բնութագրում է մարմնի աշխատանք կատարելու ունակությունը։

2.Օրինակներով ցույց տալ էներգիայի և աշխատանքի կապը

Օրինակ՝ գնդին հաղորդում ենք դեպի չորսուն ուղղված v արագություն : Հարվածելով չորսուին՝ գունդը տեղափոխում է այն և կատարում որոշակի աշխատանք:

3.Ի՞նչ միավորներով է չափվում էներգիան միավորների ՄՀ-ում:

Գիտության պատմության մեջ, էներգիան տարբեր միավորներով է արտահայտվել, ինչպիսին են էրգերը և կալորիաները։ Էներգիայի չափման ընդունված միավորը Միավորների ՄՀ-ում ջոուլն է։ Բացի ջոուլից, էներգիայի միավորներ են կիլովատտ-ժամը (ԿՎտժ) և բրիտանական ջերմային միավորը ։ Սրանք երկուսն էլ ջոուլից մեծ միավորներ են։ Մեկ ԿՎտժ-ը հավասար է 3.6 միլիոն ջոուլի։

4.Մեխանիկական էներգիայի տեսակները

Դիտարկում են մեխանիկական էներգիայի երկու տեսակ` մարմինների շարժմամբ պայմանավորված էներգիա, որն անվանում ե կինետիկ էներգիա, մարմինների փոխազդեցությամբ պայմանավորված էներգիա, որն անվանում են պոտենցյալ էներգիա։

5.Ո՞ր էներգիան են անվանում կինետիկ

Կինետիկ էներգիան սահմանվում է որպես էներգիա, որը կապված է շարժման կամ շարժվող իրերի հետ:Օրինակ, երբ ինքնաթիռը թռիչքի մեջ է, օդանավը մեծ արագությամբ շարժվում է օդում՝ ուժ գործադրելով իր շրջապատի վրա և առաջացնելով փոփոխություններ։

6.Ի՞նչ մեծություններից է կախված մարմնի կինետիկ էներգիան ,որ բանաձևով է որոշվում։

  Կինետիկ էներգիան կախված է մարմնի զանգվածից և արագությունից:

E_k=1/2mv²

7.Երբ է մարմնի կինետիկ էներգիան զրո

Դադարի վիճակում

8.Որ էներգիան են անվանում  պոտենցիալ,

Պոտենցիալ էներգիան սկալյար ֆիզիկական մեծություն է, կոնսերվատիվ ուժերի դաշտում գտնվող համակարգի լրիվ մեխանիկական էներգիայի մի մասը։

9.բերել պոտենցիալ էներգիայով օժտված մարմինների օրինակներ

Ճկված քանոնը, ամբարտակի ետևում  ամբարված ջուրը և գլանի մեջ սեղմված օդը օշտված են պոտենցիալ Էներգիայով:

10.Ինչ բանաձևով է որոշվում Երկրի մակերևույթից որոշակի բարձրությամբ մարմնի պոտենցիալ էներգիան

Eպ=mgh

11.Որ մեծություն է կոչվում մարմնի լրիվ մեխանիկական էներգիա:

Մարմինը միաժամանակ կարող է ունենալ և՛ կինետիկ, և՛ պոտենցիալ էներգիա։h բարձրության վրա արագությամբ շարժվող մարմնի լրիվ մեխանիկական էներգիան՝

Eլր=mv22+mgh

12.Ձևակերպիր լրիվ մեխանիկական էներգիայի պահպանման օրենքը

Eլր=mv22+mgh

Յուրաքանչյուր փակ համակարգում, որտեղ գործում են միայն պոտենցիալային ուժեր:

1․ Գրել անկյան կիսորդի հատկությունը։

Անկյան կիսորդի ցանկացած կետ հավասարահեռ է անկյան կողմերից:

2․ Թվարկել եռանկյան նշանավոր կետերը։

Կիսորդների հատման կետը

Միջնագծերի հատման կետ(ծանրության կենտրոն)

Բարձրությունների հատման կետը (օրթոկենտրոն)

Միջնուղղահայացների հատման կետը

3․ Եռանկյան մեջ տարված են միջնագծեր և բարձրություններ: Դրանց վերաբերյալ թվարկված պնդումներից որ՞ն է ճիշտ:

ա Եռանկյան բարձրությունները հատվելիս բաժանվում են 4:1 հարաբերությամբ հատվածների:

բ Եռանկյան միջնագծերը հատվելիս բաժանվում են 2:1 հարաբերությամբ հատվածների:

գ Եռանկյան միջնագծերը հատման կետով բաժանվում են 3:2 հարաբերությամբ հատվածների:

դ Բոլոր պնդումներն էլ սխալ են:

4․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  ներգծյալ։

Այն շրջանագիծը որը շոշափում է բազմանկյան բոլոր կողմերը։

5․ Նշել եռանկյունները, որոնց արտագծված է շրջանագիծ:

ա) PRT

բ) EFG

գ) KLM

դ) MNL

ե) ABC

զ) DEF

6․ ABC հավասարասրուն եռանկյան AB և BC կողմերին տարված բարձրությունները հատվում են M կետում: BM ուղիղը AC հիմքը հատում է N կետում: Որոշիր NC, եթե AC=36սմ

Քանի որ BN-ը անցնում է մյուս երկու բարձրությունների հատման կետով => ինքն էլ է բարձրություն։ Քանի որ հավասարասրուն եռանկյուն է => BN բարձրությունը նաև միջնագիծ է => NC=36:2=18

7․ Հաշվել քառանկյան անհայտ կողմը, եթե նրան ներգծված է շրջանագիծ: FG=10սմ, EH=15սմ, HG=12սմ

Ըստ քառանկյանը ներգծած շրջանագծի հատկության EF=10+15-12=13սմ

Թեմա՝ Իրական թվեր» թեմայի ամրապնդում։

Առաջադրանքներ։

1․ Պարզել a³b⁵c⁶d⁹ արտահայտության նշանը, եթե a>0,b<0,c<0,d>0
a³b⁵c⁶d⁹=(+)⋅(−)⋅(+)⋅(+)

Բացասական

2․ Գրել տրված թվի մոտավոր արժեքը պակասորդով՝ մինչև 0,01 ճշտությամբ՝

ա) 1.73121314151617≈1.73

բ) 3.84752136124584≈3.85

գ) 5.54210362151617≈5.54

3․ Տրված թվերը կլորացնելով 0,1 ճշտությամբ` գտնել նրանց մոտավոր գումարը.

ա) 3,288 + 0,123 = 3.4

բ) 0,100100010… + 0,238 = 0.3

գ) -1, 236 + 2, 555 = 1.4

դ)2, 7(3) + 3 ,(42) = 6.1

4․ Մինչև 0,01 ճշտությամբ կլորացնել թվերը և հաշվել նրանց մոտավոր գումարն ու տարբերությունը, եթե

ա) a=0,657 b=0,1բ) = 0.51
բ) a=5,4879  b=-0,250145 = 5.74
գ) a=-0,078 b=-0,682 = 0.60
դ) a=5,(7)  b=6,(5) = -0.88

5. Նշել մի որևէ թիվ, որը գտնվում է տված թվերի միջև:

ա) a=5,66 b=5,73
բ) a=4,5 b=4,(5)    գ) a=-2,27  b=-2.26

Թեմա՝ Ներգծյալ շրջանագիծ

Եթե բազմանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ բազմանկյան ներգծյալ շրջանագիծ:

Ներգծված շրջանագծի կենտրոնը պետք է հավասարահեռ լինի բազմանկյան կողմերից, այսինքն լինի կիսորդների հատման կետում:

Եթե քառանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ քառանկյան ներգծյալ շրջանագիծ:

Ոչ բոլոր քառանկյուններն ունեն ներգծյալ շրջանագիծ, քանի որ՝ չորս անկյունների կիսորդները կարող են նույն կետում չհատվել: 

Եթե քառանկյանը ներգծվել է շրջանագիծ, ապա քառանկյան հանդիպակաց կողմերի գումարները հավասար են՝  a+c=b+d:

Քառանկյան յուրաքանչյուր կողմ ներկայացնենք երկու հատվածների գումարի տեսքով՝ AB=AK+KB, BC=BL+LC, CD=CM+MD, և AD=DN+NA: Քանի որ, նույն կետից շրջանագծին տարված շոշափողների հատվածները հավասար են, ապա՝ AB+CD=BC+AD:

Այս հատկությունը կարելի է օգտագործել, որպես հայտանիշ, որի միջոցով կարելի է պարզել, թե ո՞ր քառանկյուններն ունեն ներգծյալ շրջանագիծ:

Փորձենք ուղղանկյանը ներգծել շրջանագիծ։Քանի որ ուղղանկյան հանդիպակաց կողմերի գումարը հավասար չէ,ապա չենք կարող ներգծել շրջանագիծ։

Եթե քառանկյան հանդիպակաց կողմերի գումարները հավասար են, ապա այդ քառանկյունն ունի ներգծյալ շրջանագիծ:

Քանի որ եռանկյան անկյունների կիսորդները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի ներգծյալ շրջանագիծ:

Քանի որ, ցանկացած եռանկյան անկյունների կիսորդները հատվում են եռանկյան ներսում, ապա ներգծյալ շրջանագծի կենտրոնը միշտ գտնվում է եռանկյան ներսում:

Հարցեր և առաջադրանքներ

1․ Ո՞ր  շրջանագիծն  է  կոչվում  բազմանկյանը  ներգծյալ։

Եթե բազմանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ բազմանկյան ներգծյալ շրջանագիծ:

 2․ Քանի՞  շրջանագիծ  կարելի  է  ներգծել  տրված  եռանկյանը:

1 շրջանագիծ

3․GEOGEBRA ծրագրով գծիր եռանկյուն, ներգծիր եռանկյանը շրջանագիծ, նկարը ցույց տուր։

4․Շրջանագծին արտագծած հավասարասրուն սեղանի հիմքերը հավասար են 4 սմ և 9 սմ։ Գտնել սեղանի պարագիծը։

26սմ

5․Ներգծյալ շրջանագծի շոշափման կետում հավասարասրուն եռանկյան սրունքը տրոհվում է 3 սմ և 4 սմ երկարությամբ հատվածների՝ հաշված հիմքից: Գտե՛ք այդ եռանկյան պարագիծը:

34սմ

6․ Գտե՛ք 6 սմ և 8 սմ էջերով և 10սմ ներքնաձիգով ուղղանկյուն եռանկյանը ներգծած շրջանագծի շառավիղը:

2սմ

7․ Ուղղանկյուն եռանկյան ներքնաձիգը 13սմ է, իսկ էջերի գումարը՝ 17սմ: Գտե՛ք եռանկյան ներգծյալ շրջանագծի շառավիղը:

2սմ

8․ Ուղղանկյուն եռանկյան ներքնաձիգը 15 սմ է, իսկ պարագիծը՝ 36սմ: Գտե՛ք այդ եռանկյան ներգծյալ շրջանագծի շառավիղը:

3սմ

Թեմա՝ Եռանկյան նշանավոր կետերը

Թեորեմ 1: Անկյան կիսորդի ցանկացած կետ հավասարահեռ է անկյան կողմերից:

Թեորեմ 2 (հակադարձ): Եթե անկյան մեջ ընկած կետը հավասարահեռ է անկյան կողմերից, ապա այն ընկած է անկյան կիսորդի վրա: 

Թեորեմ 3: Հատվածի միջնուղղահայացի ցանկացած կետ հավասարահեռ է հատվածի ծայրակետերից:

Թեորեմ 4 (հակադարձ): Եթե կետը հավասարահեռ է հատվածի ծայրակետերից, ապա այն ընկած է հատվածի միջնուղղահայացի վրա:

Եռանկյան առաջին նշանավոր կետը՝ կիսորդների հատման կետը

Թեորեմ 5: Եռանկյան անկյունների կիսորդները հատվում են միևնույն կետում:

AN -ը և BM -ը կիսորդներ են, O -ն նրանց հատման կետն է: Այս կետը եռանկյան ներգծյալ շրջանագծի կենտրոնն է և միշտ ընկած է եռանկյան մեջ:

Եռանկյան երկրորդ նշանավոր կետը՝ կողմերի միջնուղղահայացների հատման կետը

Թեորեմ 6: Եռանկյան կողմերի միջնուղղահայացները հատվում են միևնույն կետում:

Դիցուք O կետը AB և BC կողմերի միջնուղղահայացների հատման կետն է: Քանի որ այն հավասարահեռ է A, B և B, C կետերից, ապա, ըստ Թեորեմ 4-ի, այն ընկած է նաև AC կողմի միջնուղղահայացի վրա:

Այս կետը եռանկյան արտագծյալ շրջանագծի կենտրոննէ: Եթե եռանկյունը սուրանկյուն է, ապա կետը ընկած է եռանկյան մեջ, եթե եռանկյունը բութանկյուն է, ապա այն ընկած է եռանկյունից դուրս և, եթե եռանկյունը ուղղանկյուն է, ապա այն ընկած է ներքնաձիգի վրա:

Եռանկյան երրորդ նշանավոր կետը՝ միջնագծերի հատման կետը

Թեորեմ 7: Եռանկյան միջնագծերը հատվում են միևնույն կետում, որը յուրաքանչյուր միջնագիծը բաժանում է 2 : 1 հարաբերությամբ հատվածների՝ հաշված գագաթից:

Միջնակետերի հատման կետն անվանում են եռանկյան ծանրության կենտրոն:

Եռանկյան չորրորդ նշանավոր կետը՝ բարձրությունների հատման կետը

Թեորեմ 8: Եռանկյան բարձրությունները (կամ նրանց շարունակությունները) հատվում են միևնույն կետում:

Բարձրությունների հատման կետն անվանում են եռանկյան օրտոկենտրոն:

Հարցեր և առաջադրանքներ

1․ Գրել չորս նշանավոր կետերը։

• ներգծյալ շրջանագծի կենտրոն
•  արտագծյալ շրջանագծի կենտրոն
• ծանրության կենտրոն
• եռանկյան օրտոկենտրոն

2․ Լուծել խնդիրը

3․ Լուծել խնդիրը

AO=10 սմ

4․ Լուծել խնդիրը

ա)8,5։2=4,25
AD=4,25 սմ
CD=4,25 սմ

բ)3,2×2=6,4
AD=6,4 սմ
CD=6,4 սմ

 1.Նկարագրե՛ք և գնահատե՛ք Ադրբեջանի աշխարհագրական դիրքը:

Ադրբեջանի աշխարհագրական դիրքն առաջարկում է և՛ դրական, և՛ մինուսներ. Դրական կողմը մեծ էներգետիկ ռեսուրսների հասանելիությունն է. լինելը մեծ, հզոր երկրների հենց հարեւանությամբ; Եվ Եվրոպայի և Ասիայի միջև սահմանը խճողվելը բոլորը խթանում են երկրի աշխարհաքաղաքական ազդեցությունը:

2. Գնահատե՛ք Կասպից ծովի նշանակությունը Ադրբեջանի համար: 

Ամփոփելով ասեմ, որ Ադրբեջանի տնտեսությունը, աշխարհաքաղաքականությունը և մշակույթը Կասպից ծովը դարձնում են նրա համար գերակա նշանակություն: Ծովն ապահովում է էներգիա և հարստություն, օգնում է երկրին աճել և զարգանալ, ինչպես նաև փրկօղակ է Եվրոպա արտահանման համար և որպես կամուրջ Եվրոպայից դուրս: Ծովը նաև բնապահպանական մարտահրավերներ է ստեղծում, որոնք հարյուր հազարավոր տարիների ընթացքում Կասպից ծովում իրավիճակը բավականին յուրահատուկ են դարձրել:

3. Գնահատեք Ադրբեջանի բնական պայմանները և ռեսուրսները՝ տնտեսության տարբեր ոլորտների տեսանկյունից:

Բնական գազ, նավթ, գույնավոր մետաղններ։