Թեմա՝ Առանցքային և կենտրոնային համաչափություն։

Առանցքային համաչափության ժամանակ հարթության յուրաքանչյուր կետի որոշակի օրենքով համապատասխանության մեջ է դրվում հարթության մեկ այլ կետ:

Օրենքը հետևյալն է:

1. M կետից տարվում է ուղղահայաց համաչափության առանցքին (ուղղին) և ստացվում է P կետը՝ ուղղահայացի հատման կետը համաչափության առանցքի հետ:  

2. Ուղղահայացի վրա տեղադրվում է PM1=PM հատվածը և գտնվում է M1 կետը:

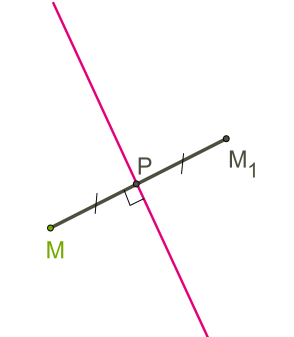
Այսպիսով, հարթության ցանկացած M կետի համար գտնվում է միակ՝ նրան համաչափ M1 կետը:

M և M1 կետերը կոչվում են համաչափ տրված առանցքի նկատմամբ (համաչափության առանցքի), եթե

1) MM1 հատվածը ուղղահայաց է համաչափության առանցքին,

2) համաչափության առանցքը անցնում է MM1 հատվածի միջնակետով՝  PM1=PM

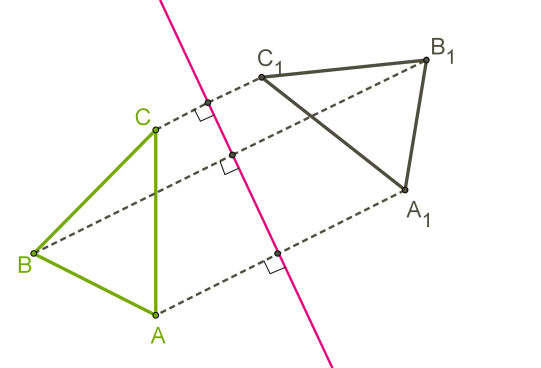
Բազմանկյունները համաչափ արտապատկերելու համար բավական է արտապատկերել նրանց գագաթները և միացնել ստացված կետերը:  

Ուշադրություն

Առանցքային համաչափության ժամանակ

1. հատվածը գալիս է նույն երկարության հատվածի (կետերի միջև երկարությունները պահպանվում են),

2. ճառագայթը գալիս է ճառագայթի, ուղիղը՝ ուղղի,

3. պատկերները գալիս են հավասար պատկերների:

Երբեմն համաչափության երևույթներ հանդիպում ենք նաև բնության մեջ:

Կենտրոնական համաչափության ժամանակ M կետը արտապատկերվում է M1 կետի հետևյալ օրենքով:

1. M և O (համաչափության կենտրոն) կետերով տանում ենք ուղիղ:

2. Ուղղի վրա տեղադրում ենք OM1=OM հատվածը և գտնում ենք M1 կետը:

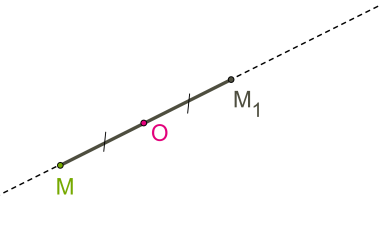
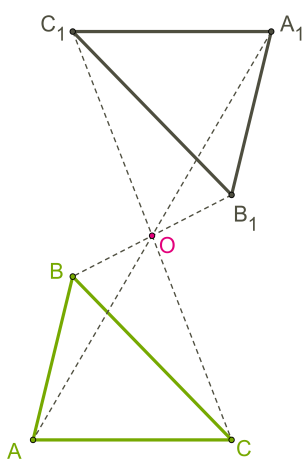
M և M1 կետերը կոչվում են համաչափ O կետի նկատմամբ, եթե O -ն MM1 հատվածի միջնակետն է՝  OM1=OM

Բազմանկյունները համաչափ արտապատկերելու համար բավական է արտապատկերել նրանց գագաթները և միացնել ստացված կետերը: 

Ուշադրություն

Ինչպես և առանցքային համաչափության ժամանակ, այս դեպքում ևս

1. հատվածը գալիս է նույն երկարության հատվածի (կետերի միջև երկարությունները պահպանվում են),

2. ճառագայթը գալիս է ճառագայթի, ուղիղը՝ ուղղի,

3. պատկերները գալիս են հավասար պատկերների:

Նկարում պատկերված ծառերը նույն գույնի և չափի են, սակայն ունեն մի կարևոր տարբերություն. առաջին ծառի ձախ և աջ մասերն իրար նման են, մինչդեռ երկրորդ ծառի ձախ և աջ մասերն իրարից զգալի տարբերվում են։

Բնության մեջ հաճախակի են հանդիպում համաչափության առանցք ունեցող օբյեկտներ՝ կենդանիներ, բույսեր և այլն։ Մարդիկ և կենդանիների մեծ մասն ունեն համաչափության առանցքներ։ Ոչ բոլոր կենդանիներն ունեն համաչափության առանցք, օրինակ խխունջը չունի։ Որոշ բույսեր ունեն մեկից ավելի համաչափության առանցք, օրինակ երիցուկը։ «Ամենահամաչափ» պատկերը շրջանագիծն է, այն ունի անվերջ քանակությամբ համաչափության առանցքներ՝ կենտրոնով անցնող ցանկացած ուղիղ համաչափության առանցք է։ Անմոռուկը համաչափության առանցքները 5-ն են։

Առանցքային համաչափությամբ օժտված պատկերներ։

Առաջադրանքներ։

1. O կետը AL հատվածը բաժանում է երկու հավասար մասերի: Գտնել  հատվածի միջնակետի նկատմամբ համաչափ կետեր:

AL,BK,CJ,DI,EH,FG

2. Տրված է AL հատվածը: Գտնել D կետի նկատմամբ համաչափ կետերը:

CE,BF,AG

3. Ո՞ր կետն է C կետին համաչափ՝ (0;−4) կետի նկատմամբ:

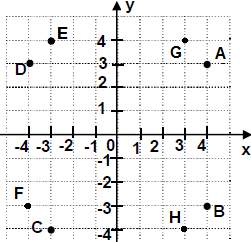
H

4. Գտնել Оx առանցքի նկատմամբ B կետին համաչափ կետը:

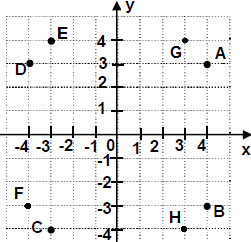
D,A

5․ Կոորդինատային հարթության վրա կառուցիր հետևյալ գագաթներով եռանկյունը` A(9; 3), B(3;−9) և C(−9; −3)։ Կառուցել A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> եռանկյունը, որը համաչափ է տրվածին` y=3 ուղղի նկատմամբ: Գրել  A₁B₁C₁ եռանկյան գագաթների կոորդինատները:

6․ Կոորդինատային հարթության վրա գծիր քառանկյուն, որի գագաթները հետևյալ կետերն են՝

A(18; 6), B(6; −18), C(−18; −6) և D(−6; 18)։ Գծել A₁B₁C₁D₁ քառանկյունը, որը համաչափ է տրված քառանկյանը՝ (0;0) կետի նկատմամբ: Գրել  A₁B₁C₁D₁ քառանկյան գագաթները:

7․ Նշել այն պատկերները, որոնք ունեն համաչափության կենտրոն:

• Իննանկյուն
• Սեղան
• Քառակուսի
• Ուղղանկյուն

8․ Նշել այն պատկերները, որոնք ունեն համաչափության առանցք: 

• Շրջան
• Քառանկյուն
• Եռանկյուն
• Շեղանկյուն

9․ Նշել այն տառերը և թվերը, որոնց տեսքն ունի համաչափության առանցք:

186.Ի՞նչ ընդհանրությամբ են խմբավորվել տրված բայերը:

Ա. Կիրառել, խմել, հնարել, բացատրել, գրավել, հասնել, լցնել, թռչել, սառչել:

Բ. Գնալ, գգալ, խոյանալ, ընթանալ, վախենալ, կամենալ, տզզալ, շրխկալ:

187.Տրված արմատներից բայեր կազմի՛ր և ընդգծի՛ր արմատի և ել կամ ալ վերջավորության միջև եղած մասը:
Օրինակ`

տես — տեսնել, բարձր — բարձրանալ:

Ա. Ընկեր, թանձր, խոր:

Բ. Վախ, կամ, մոտ:

Գ. Հաս, անց, հագ:

Դ-. Թիռ, սառ, կիպ:

188.Տրված բայերը պատճառական դարձնող ածանցները թվի՛ր:

Մեծացնել, հեռացնել, գգացնել, վախեցնել, հիշեցնեյ, թռցնել, տեսցնել:

189.Տրված բայնրի անցյալ ժամանակը կազմի՛ր և պարզի՛ր, թե ինչպե՛ս

է փոխվում ընդգծված բայածանցներից յուրաքանչյուրը:

հագենալ — հագեցել է – են-ը դառնում է եց:

Հեռանալ, մոտենալ, դալկանալ, ամրանալ, գտնել, տեսնել, թռն ել, փախչել, հասցնել, մեծացնել:

190.Տրված բայերի անցյալ ժամանակը կազմելու միջոցով պարզի՛ր, թե ընդգծվածները ո՛ր բառերի մեջ են արմատի մասեր և որտեղ` բայ կազմող ածանցներ (կարող են փոփոխվել կամ դուրս գալ):

կպչել- կպել է, հաչել — հաչել է  (կպչել բառի մեջ չ-ն ածանց է):
Հանել, վանել, բարձրանալ, մանկանալ, հենել, վախենալ) մեռնել, բռնել, թռչել, խաչել, հառաչել:

191.Ընդգծի՛ր տրված անորոշ, անկատար, վաղակատար, հարակատար դերբայների ա)ել, ալ, բ)ում, գ)ել, դ)ած վերջավորություններից առաջ ընկած մասերը (հիմքերը) և պատասխանի՛ր հարցերին:

Ա Զգալ, ծերանալ, կպչել, տեսնել:
Բ. Զգում (է), ծերանում (է), կպչում (է), տեսնում (է):
Գ. Զգացել (է), ծերացեք (է), կպել (է), տեսել (Է է):
Դ. Զգացած, ծերացած, կպած, տեսած:

Ո՞ր դերբայների հիմքերն են իրար նման:
Ո՞ր հիմքերը կարելի է կոչել անցյալի հիմք:
Ինչպե՞ս կանվանես մյուս հիմքը:

Անորոշ դերբայ — սիրել, կարդալ, թռչել
Ենթակայական դերբայ
Հարակատար դերբայ
Համակատար դերբայ
Անկատար դերբայ
Վաղակատար դերբայ
Ապակատար դերբայ
Ժխտական դերբայ