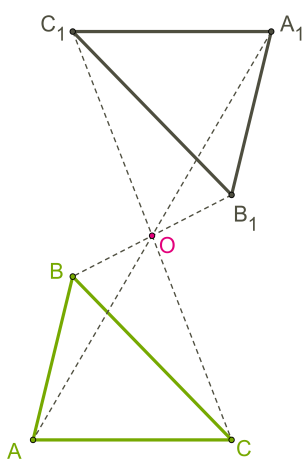
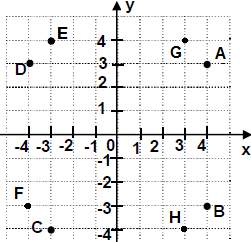
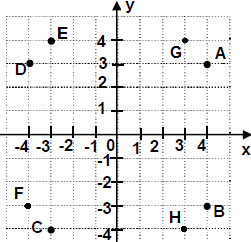
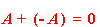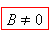Թեմա՝ Հանրահաշվական կոտորակներ եւ նրանց հատկությունները։

Թվային արտահայտությունը կազմվում է թվերից, թվաբանական գործողությունների նշաններից և փակագծերից:

Թվային արտահայտության գործողությունների արդյունքում ստացված թիվը կոչվում է թվային արտահայտության արժեք:

Եթե արտահայտության մեջ պատահում է բաժանում զրոյի վրա, ապա այդ արտահայտությունն արժեք (իմաստ) չունի: Զրոյի վրա բաժանել չի կարելի:  

(−3)²+5⋅0,2 թվային արտահայտության արժեքը հավասար է 10-ի:

(7−(−2)5+(6⋅4))/0 արտահայտությունն արժեք չունի:

Եթե թվային արտահայտությունը պարունակում է նաև տառեր (կամ միայն տառեր), ապա այն կոչվում է հանրահաշվական արտահայտություն:

(−3)²+5x; 3a+4b; (2x−6)/3 արտահայտությունները հանրահաշվական են:

Հանրահաշվական կոտորակ կոչվում է A/B տեսքի արտահայտությունը, որտեղ A-ն որևէ բազմանդամ է, իսկ B-ն՝ ոչ զրոյական բազմանդամ:

Հանրահաշվական կոտորակը բազմանդամի և ոչ զրոյական բազմանդամի քանորդ է:

x/(x−3); (b−1)/(b+6); (1+x³)(x²+1); (y+2)/(y²−6y+6) արտահայտությունները հանրահաշվական կոտորակներ են:

Մեկ փոփոխականով արտահայտության որոշման տիրույթ կոչվում է փոփոխականի բոլոր այն արժեքների բազմությունը, որոնց համար արտահայտությունն իմաստ (արժեք) ունի:   

Որոշման տիրույթի ցանկացած կետում արտահայտությունն ունի արժեք:  

Օրինակ` Գտնենք (x−3)/x(x+8) հանրահաշվական կոտորակի որոշման տիրույթը:

Լուծում. (x−3)/x(x+8) հանրահաշվական կոտորակը որոշված է x փոփոխականի բոլոր այն արժեքների համար, որոնց դեպքում կոտորակի x(x+8) հայտարարը հավասար չէ 0-ի: Հետևաբար որոշման տիրույթին չպատկանող x -ի արժեքները գտնելու համար պետք է լուծել հետևյալ հավասարումը՝

x(x+8)=0

Յուրաքանչյուր արտադրիչ հավասարեցնում ենք զրոյի՝

x=0 և x+8=0

x=−8

Պատասխան՝ տրված հանրահաշվական կոտորակի որոշման տիրույթը բաղկացած է բոլոր իրական թվերից, բացի 0 և −8 թվերից:

Հանրահաշվական կոտորակի որոշման տիրույթը բաղկացած է բոլոր այն իրական թվերից, որոնց դեպքում կոտորակի հայտարարը հավասար չէ 0-ի:

Հանրահաշվական կոտորակների հիմնական հատկությունը

Հանրահաշվական կոտորակի արժեքը չի փոխվի, եթե նրա համարիչը և հայտարարը բազմապատկենք միևնույն արտահայտությամբ, որի արժեքը զրոյից տարբեր է:

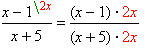
Հանրահաշվական կոտորակների հետ գործողություններ կատարելիս միշտ ենթադրվում է, որ գործողությունները կատարվում են որոշման տիրույթում (թույլատրելի արժեքների հետ):  

Եթե տրված է A հանրահաշվական կոտորակը, ապա այն −1-ով բազմապատկելով, ստանում ենք՝ (−1)⋅A=−A

A և −A կոտորակները կոչվում են փոխադարձ հակադիր, եթե դրանց գումարը հավասար է 0-ի, այսինքն՝ 

Ինչպես և հակադիր թվերը, հակադիր հանրահաշվական կոտորակները ևս տարբերվում են միայն նշաններով:

Հաճախ հանրահաշվական կոտորակների հետ գործողություններ կատարելիս, պետք է լինում փոխարինել կոտորակի համարիչը կամ հայտարարը հակադիրով: Սակայն, որպեսզի կոտորակի արժեքը չփոխվի, պետք է հետևել նշանի փոփոխության կանոններին՝

կոտորակի արժեքը չի փոխվի, եթե 

— փոխենք համարիչի և հայտարարի նշանները,

— փոխենք համարիչի և ամբողջ կոտորակի նշանները,  

— փոխենք հայտարարի և ամբողջ կոտորակի նշանները:

Եթե A-ով և B-ով նշանակենք հանրահաշվական կոտորակի համարիչն ու հայտարարը, ապա նշանի փոփոխման կանոնը կարելի է գրել հետևյալ կերպ՝  

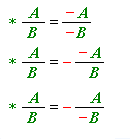
Կանոնը ուժի մեջ է միայն այն դեպքում, երբ 

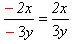
Այս հավասարությունները կարելի է ստուգել ցանկացած արժեքի համար հանրահաշվական կոտորակների որոշման տիրույթից:

Հանրահաշվական կոտորակը կրճատելու համար պետք է կոտորակի համարիչը և հայտարարը վերլուծել արտադրիչների: Եթե պարզվի, որ համարիչն ու հայտարարն ունեն ընդհանուր արտադրիչներ, ապա դրանք կարելի է կրճատել:

Արտադրիչների վերլուծման օրինակներ՝

— ընդհանուր արտադրիչի դուրս բերումը փակագծերից,

— կրճատ բազմապատկման բանաձևերի օգտագործումը,

— խմբավորման եղանակ:

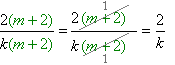
Առաջադրանքներ։

1․ Գտնել  (c−15)/c հանրահաշվական կոտորակի արժեքը, եթե c=16
1/16

2․ Հետևյալ կոտորակներից ո՞րն է հավասար 3/(x−15)-ի: Ընտրել պատասխանի ճիշտ տարբերակը:

• −(x+15)/−3
• −3/−(x−15)
• (x−15)/−3
• 3/(15−x)
• 
  −3/(15−x)

3․ Կրճատել կոտորակը՝

1. x+y/2ax
2. 1
3. 2/5
4. 1/2
5. (x-y)²/4xy
6. 5m/7n(a-b)

4․ Հետևյալ կոտորակները բերել 20 x²y հայտարարի

1. x²/20x²y
2. 100y/20yx²
3. 7x²y/20x²y
4. 110yx / 20yx²
5. 12x/20x²y

5․ A միանդամը կամ բազմանդամը ընտրեք այնպես, որ ստացվի ճիշտ հավասարություն՝

A = 4

A = 2(x-y)

6․ Կրճատել կոտորակները․

1. a-b/c+d
2.a+b/m+n
3.x²/x+y
4.ab/b
5.m/m-n
6.a-b/x+y

1.Որ շարժումն են      անվանում   շրջանագծային հավասարաչափ շարժում:

Շրջանագծային հավասարաչափ շարժումը այնպիսի շարժում է, երբ մարմինը շարժվում է շրջանագծի վրա՝ առանց իր արագության փոփոխման։ Այս շարժման ժամանակ մարմնի անկյունային արագությունը մշտական է և նույնն է բոլոր դիրքերում։ Այդպիսի շարժման դեպքում մարմնի արագությունը միշտ ուղղված է դեպի շրջանի կենտրոն, իսկ արագության մոդուլը չի փոխվում։

2.Ինչ ուղղություն ունի արագությունը շրջանագծային հավասարաչափ շարժման դեպքում:բերել օրինակներ

Շրջանագծային հավասարաչափ շարժման դեպքում արագությունը միշտ ուղղված է շրջանի շոշափող գծին, որին պարսպվում է մարմնի շարժման ընթացքը: Այն միտված է դեպի շարժվող մարմնի դիրքը և հակառակ ուղղությամբ է, քան կենտրոնից դուրս գնացող ուժի համար: Օրինակ՝ արբանյակների շարժումը Երկրին կամ ավտոմեքենայի շարժումը՝ ճեղքումով կամ շրջապատելով շրջանը։ Իհարկե, նույնիսկ եթե արագությունը կայուն է, ուղղությունը փոփոխվում է ըստ մարմնի շարժման ծալող գծի։

3.Ինչ է պտտման պարբերությունը:

Պտտման պարբերությունը (T) ժամանակահատվածն է, որը պետք է անցնի, որպեսզի մարմինը կատարի մեկ ամբողջ պտույտ (շրջանագծի շուրջ): Այն կցվում է անկյունային արագության հետ և հաճախ չափվում է վայրկյաններով։

4.Ինչ է պտտման հաճախությունը,և որն է նրա միավորը:

Պտտման հաճախությունը (f) այն փոփոխություն է, որը ցույց է տալիս, թե քանի պտույտ է կատարում մարմինը մեկ վայրկյանում։ Այն հաշվարկվում է որպես մեկ վայրկյանի ընթացքում կատարած պտույտների քանակը։ Պտտման հաճախությունը հակառակ հարաբերություն ունի պտտման պարբերության (T) հետ՝ f=1Tf=T1​։ Պտտման հաճախության միավորը Hertz (Hz) է, որը նշանակում է մեկ պտույտ մեկ վայրկյանում։ Օրինակ, եթե մարմինը կատարում է 5 պտույտ մեկ վայրկյանում, ապա դրա պտտման հաճախությունը կլինի 5 Hz։

5.Գրել և բացատրել պտտման պարբերության և հաճախության կապն արտահայտող բանաձևը:

Պտտման պարբերության (T) և պտտման հաճախության (f) կապը արտահայտվում է հետևյալ բանաձևով՝ T=1fT=f1​, որտեղ TT պտտման պարբերությունն է (ժամանակը, որում մարմինը կատարում է մեկ պտույտ), իսկ ff պտտման հաճախությունն է (պտույտների քանակը մեկ վայրկյանում)։ Այս բանաձևը ցույց է տալիս, որ որքան մեծ է պտտման հաճախությունը, այնքան փոքր է պտտման պարբերությունը, և հակառակը։

6.Ինչպես կարելի է հաշվել շրջանագծով հավասարաչափ շարժվող մարմնի արագությունը,եթե հայտնի են շրջանագծի շառավիղը և պտտման պարբերությունը կամ պտտման հաճախությունը։

Շրջանագծով հավասարաչափ շարժվող մարմնի արագությունը կարելի է հաշվել հետևյալ բանաձևով՝ v=2πr/Tv=2πr/T, որտեղ rr շրջանագծի շառավիղն է, TT պտտման պարբերությունը, կամ այլընտրանքային տարբերակով, v=2πrfv=2πrf, որտեղ ff պտտման հաճախությունն է։ Այս բանաձևերը ցույց են տալիս, որ մարմնի արագությունը կախված է շրջանի շառավիղից և պտտման պարբերությունից կամ հաճախությունից։

Աշխատանքի նպատակը․

1․Համոզվել,որ ուսումնասիրվող շարժումը հավասարաչափ արագացող է։

2․Կարողանալ ճանապարհի և ժամանակի օգնությամբ որոշել թեք ճոռով շարժվող գնդիկի շարժման արագացումը ։

3․Հաշվելով շարժման ճանապարհը և արագացումը կարողանալ հաշվել ժամանակը։

4․Սովորողների մոտ զարգացնել փորձարարական և հաշվողական հմտությունները։

Աշխատանքը կատարելու համար սովորողը պետք է իմանա․

1․Հավասարաչափ շարժման հիմնական բանաձևերը․

V=at S=at²/2 ՝ այս բանաձևից a= 2S/t²

2․Արագացման սահմանումը,բանաձև,միավորը։

Անհրաժեշտ սարքեր և նյութեր․մետաղե ճոռ․պողպատե գնդիկ,վայրկենաչափ․մոտաղյա բաժակ,չափաժապավեն քանոն,ամրակալան։

Փորձի ընթացքը․

Ամրակալանին ամրացրու ճոռը,որոշակի անկյան տակ։Ճոռի հիմքին տեղավորիր մետաղյա բաժակը։Չափիր ճոռի երկարությունը։Դա կլինի այն ճանապարհը(S),որը կանցնի գնդիկը փորձի ժամանակ։Բաց թող գնդիկը ճոռի վերևի մասից, և միաժամանակ աշխատեցրու վայրկենաչափը։Երբ գնդիկը կբախվի արգելակին կանգնեցրու վայկենաչափը և գրանցիր շարժման ժամանակը՝կլորացնելով վայրկյանի տասնորդական մասով։Փորձը կրկնիր երեք անգամ և հաշվիր չափված ժամանակների միջին արժեքը՝t=(t₁+t₂+t₃)/3:Հաշված ժամանակը ընդունիր որպես գնդիկի շարժման ժամանակ։Վերևի բանաձևով հաշվիր արագացումը՝ a= 2S/t²

Փորձ 1

S= 1.1մ | t=(t₁+t₂+t₃)/3= | t=3.6/3=1.2վ

t₁= 1.3վ | a= 2S/t² = | a=2.2/1.44 մ/վ

t₂=1․2վ |

t₃=1․1վ |

——————-

a-? Պատ՝․2․2/1,69 մ/վ

Փորձ 2

S=0,5մ | t=(t₁+t₂+t₃)/3= |t=(0.8+0.9+0.8)/3=0.8վ

t₁= 0․8վ | a= 2S/t² = | a=1/0.64 մ/վ

t₂=0․9վ |

t₃=0․8վ |

——————-

a-? Պատ․՝ 1/0,64 մ/վ

Փորձ 3

S=0․25մ | t=(t₁+t₂+t₃)/3= |t=(0.8+0.7+0.6)/3=0.7վ

t₁=0․8վ | a= 2S/t² = | a= 0.5/0.49 մ/վ

t₂=0․7վ |

t₃=0․6վ |

——————-

a-? Պատ․՝ 0.5/0.49 մ/վ

Այժմ նույւն փորձը ,նույն կերպ կրկնիր S-ի համար ընտրելով երկու ուրիշ չափեր։

Կատարածդ փորձերից արա վերջնական եզրակացություն,գնդիկի շարժումը թեք ճոռով———

1․հավասարաչափ է։

2․անհավասարաչափ արագացող է։

3․ հավասարաչափ արագացող է։Ինչո՞ւ։

Թեմա՝ Ուղղանկյունանիստ և խորանարդ

Մեր շրջակայքի շատ առարկաներ ունեն այնպիսի զուգահեռանիստի տեսք, որի բոլոր նիստերը ուղղանկյուններ են: Այդպիսի առարկաներ են շենքերը, սենյակները, տուփերը, պահարանները:

Զուգահեռանիստը, որի կողմնային կողերն ուղղահայաց են հիմքին կոչվում է ուղիղ զուգահեռանիստ:

Այն ուղիղ զուգահեռանիստը, որի հիմքերն ուղղանկյուններ են կոչվում է ուղղանկյուն զուգահեռանիստ կամ պարզապես՝ ուղղանկյունանիստ:

Քանի որ ցանկացած ուղիղ զուգահեռանիստի կողմնային կողերն ուղղահայաց են հիմքին, ապա ուղղանկյունանիստի կողմնային նիստերն ուղղանկյուններ են:

Ուղղանկյունանիստի բոլոր վեց նիստերը ուղղանկյուններ են:

Ուղղանկյունանիստի ընդհանուր գագաթով երեք կողերի երկարությունները անվանում են ուղղանկյունանիստի չափսեր՝ երկարություն, լայնություն, բարձրություն:

Այն ուղղանկյունանիստը, որի բոլոր կողերը հավասար են, կոչվում է խորանարդ:

Պարզ է, որ խորանարդի բոլոր նիստերը միմյանց հավասար քառակուսիներ են:

Ուղղանկյունանիստի բոլոր չորս անկյունագծերը հավասար են, հատվում են մի կետում և հատման կետում կիսվում են:

Եթե ACC₁ ուղղանկյուն եռանկյունից արտահայտենք ուղղանկյունանիստի անկյունագիծը՝ AC₁²=AC²+CC₁²,

և ADC ուղղանկյուն եռանկյունից արտահայտենք հիմքի անկյունագիծը՝ AC²=AD²+DC², ապա ստանում ենք՝ AC₁²=AD²+DC²+CC₁²

Ուղղանկյունանիստի անկյունագծի քառակուսին հավասար է նրա երեք չափսերի քառակուսիների գումարին՝ D²=a²+b²+c²

Հարցեր և առաջադրանքներ։

1․ Ո՞ր մարմինն է կոչվում ուղղանկյունանիստ։ GEOGEBRA ծրագրով գծել ուղղանկյունանիստ։

Այն ուղիղ զուգահեռանիստը, որի հիմքերն ուղղանկյուններ են կոչվում է ուղղանկյուն զուգահեռանիստ կամ պարզապես՝ ուղղանկյունանիստ:

2․ Ի՞նչ երկրաչափական պատկերներից է կազմված ուղղանկյունանիստը։

Ուղղանկյունանիստի կողմնային նիստերն ուղղանկյուններ են:

3․ Ո՞ր մարմինն է կոչվում խորանարդը։ GEOGEBRA ծրագրով գծել խորանարդ։

Այն ուղղանկյունանիստը, որի բոլոր կողերը հավասար են, կոչվում է խորանարդ:

4․ Քանի՞ նիստ, կող, գագաթ ունեն ուղղանկյունանիստն ու խորանարդը։

Ուղղանկյունանիստն ունի 12 կող, 8 գագաթ ու 6 նիստ։

Խորանարդն ունի 8 գագաթ, 12 կող, 6 նիստ։

5․ Որո՞նք են ուղղանկյունանիստի չափումները։

Ուղղանկյունանիստի երկարությունը, լայնությունը եւ բարձրությունը
ունեն ընդհանուր անվանում՝ ուղղանկյունանիստի չափումներ։

6․ Համեմատել խորանարդը և ուղղանկյունանիստը։

Նման են, որովհետև եռաչափ մարմիներ են 12 կող 6 նիստ և 8 գագաթ։ Տարբերվում են նրանով, որ ուղանկյունանիստի նիստը ուղանկյուն է, իսկ խորանարդինը քառակուսի։

7․ Տրված է հետևյալ ուղղանկյունանիստը:

Ո՞րն է ուղղանկյունանիստի անկյունագծի հաշվման բանաձևը:  Ընտրել ճիշտ բանաձև(եր)ը:

• KM²=KN²+NM²
• AM²=AD²+DC²+CM²
• BN²=BD²+DN²

8․ Հայտնի են ուղղանկյունանիստի նույն գագաթից ելնող կողերի երկարությունները՝  10 սմ,  2 սմ  և  4 սմ: Գտնել  ուղղանկյունանիստի անկյունագծի քառակուսու երկարությունը:  

AM²=AD²+DC²+CM²

AM²=10²+2²+4²

AM²=100+4+16

AM²=120

9․ Հայտնի են ուղղանկյունանիստի հիմքի կողերի երկարությունները՝ 16 սմ, 24 սմ և  ուղղանկյունանիստի  անկյունագծի երկարության քառակուսին՝ 857: Գտնել ուղղանկյունանիստի բարձրությունը:

c²=857-16²-24²

c²=857-256-576

c²=25

10․ Որոշիր խորանարդի d անկյունագիծը, եթե նրա մի նիստի մակերեսը S=49սմ²է:

d=3a²

d=49+49+49=147սմ²

Թեմա՝ Տարածական պատկերներ։ Զուգահեռանիստ

Երկրաչափության այն բաժինը, որը ուսումնասիրում է պատկերների հատկությունները տարածության մեջ, կոչվում է տարածաչափություն:

Այն պատկերը, որի ոչ բոլոր կետերն են ընկած միևնույն հարթության մեջ, կոչվում է  տարածական պատկեր:

Տարածության սահմանափակված մասը կոչվում է երկրաչափական կամ տարածաչափական մարմին, իսկ մարմինը սահմանափակող կետերի բազմությունը՝ մարմնի մակերևույթ:

Գունդը երկրաչափական մարմին է, գնդոլորտը նրա մակերևույթն է:

Պարուրաձև գիծը տարածական պատկեր է: Սակայն այն մարմին չէ:

պարուրաձև գիծ

Բուրգը երկրաչափական մարմին է, որը սահմանափակված է բազմանկյուններով:

Բազմանիստի մակերևույթը կազմող բազմանկյունները կոչվում են բազմանիստի նիստեր:

Նիստերի կողմերը կոչվում են բազմանիստի կողեր:

Կողերի ծայրակետերը կոչվում են բազմանիստի գագաթներ:

Զուգահեռանիստի սահմանումն ու հատկությունները

Զուգահեռանիստ կոչվում է այն բազմանիսը, որի բոլոր 6 նիստերը զուգահեռագծեր են:

Զուգահեռանիստն ունի 6 նիստ, 8 գագաթ և 12 կող:

Զուգահեռանիստի ընդհանուր կող ունեցող նիստերը կոչվում են կից, իսկ ընդհանուր կողեր չունեցող նիստերը՝ հանդիպակաց:

Զուգահեռանիստի հիմքեր անվանում են նիա որևէ երկու հանդիպակաց նիստերը, իսկ մնացած նիստերը՝ կողմնային նիստեր: 

Հիմքերին չպատկանող կողերը կոչվում են զուգահեռանիստի կողմնային կողեր: 

Նույն նիստում չգտնվող երկու գագաթները միացնող հատվածը կոչվում է զուգահեռագծի  անկյունագիծ: 

Զուգահեռանիստի հատկությունները:

— Զուգահեռանիստի հանդիպակաց նիստերը զուգահեռ են և հավասար:

— Զուգահեռանիստի բոլոր չորս անկյունագծերը հատվում են միևնույն կետում և այդ կետում կիսվում են: 

Հարցեր և առաջադրանքներ։

1․ Ո՞ր պատկերն է կոչվում տարածական մարմին կամ տարածական պատկեր։

Այն պատկերը, որի ոչ բոլոր կետերն են ընկած միևնույն հարթության մեջ, կոչվում է  տարածական պատկեր:

2․ GEOGEBRA ծրագրով գծել տարածական մարմին։

3․ Ի՞նչ է բազմանիստը։

Բազմանկյուններով կազմված փակ մակերևույթ, նրան երբեմն անվանում են այդ մակերևույթով սահմանափակված մարմին։

4․ Ո՞ր պատկերն է կոչվում զուգահեռանիստ, GEOGEBRA ծրագրով գծել զուգահեռանիստ։

Այն բազմանիստը որի բոլոր նիիստերը զուգահեռագծեր են կոչվում է զուգահեռանիստ։

5․ Զուգահեռանիստը քանի՞ նիստ, քանի՞ կող, քանի՞ գագաթ ունի։

Զուգահեռանիստն ունի 6 նիստ, 8 գագաթ և 12 կող:

6․ Բազմանիստների և նրանց տարրերի մասին բերված պնդումներից (սահմանումներից) ո՞րն է ճիշտ: Ընտրել ճիշտ տարբերակ(ներ)ը:

Եթե տարածական մարմնի մակերևույթը կազմված է ուղղանկյուններից, ապա այն կոչվում է բազմանիստ:

Բազմանիստի մակերևույթը կազմող բազմանկյունները կոչվում են բազմանիստի նիստեր:

Նիստերի կողմերը կոչվում են բազմանիստի կողեր:

Եթե տարածաչափական մարմնի մակերևույթը բաղկացած է բազմանկյուններից, ապա մարմինը բազմանիստ է:

7․ Զուգահեռանիստի մասին թվարկված պնդումներից ո՞րն է ճիշտ: Ընտրել ճիշտ պնդումը:

Զուգահեռանիստի հիմքը զուգահեռագիծ է:

Զուգահեռանիստ կոչվում է այն պրիզման, որի կողմնային նիստերը չորս ուղղանկյուններ են:

Զուգահեռանիստի նիստերը վեց ուղղանկյուններ են:

8․ Բերվածնկարներից ո՞րն է զուգահեռանիստը: Նշել  ճիշտ պատասխանը:

Վերջին, երրորդն է զուգահեռանիստ։

9․ Գրել զուգահեռանիստի հատկությունները։

— Զուգահեռանիստի հանդիպակաց նիստերը զուգահեռ են և հավասար:

— Զուգահեռանիստի բոլոր չորս անկյունագծերը հատվում են միևնույն կետում և այդ կետում կիսվում են: 

10․ ABCDA₁B₁C₁D₁ զուգահեռանիստի մեջ գտնել B₁C₁ -ը և DC-ն, եթե BC=7 սմ, A₁B₁=5 սմ:

B₁C₁=7սմ

DC=5սմ

1.Ի՞նչ դեր ունեն Ռուսաստանի բնական պայմաններն ու բնական ռեսուրսները երկրի զարգացման հարցում։

Ռուսաստանի բնական պայմաններն ու ռեսուրսները մեծ դեր են խաղում երկրի տնտեսական զարգացման մեջ, քանի որ երկիրը աշխարհում ունի կարևորագույն էներգետիկ, հանքային և գյուղատնտեսական ռեսուրսներ: Նավթի, բնական գազի և մետաղների հսկայական պաշարները հիմնաքար են երկրի արդյունաբերության ու էկոնոմիկայի համար: Ագրարային և անտառային ռեսուրսները նույնպես կարևոր դեր ունեն գյուղատնտեսության ու անտառային արդյունաբերության մեջ: Սակայն, բնական ռեսուրսների շահագործման հետ կապված առկա են նաև էկոլոգիական և տրանսպորտային մարտահրավերներ, որոնք պահանջում են ավելի կայուն ու արդյունավետ կառավարման մոտեցումներ:

2.Ուրվագծայի քարտեզի վրա նշել Ռուսաստանի հարևան պետությունները, ափերը ողողող ջրային ավազանները:

Ռուսաստանի ափերը ողողող ջրային ավազանները և հարևան պետությունները, միավորված միաժամանակ գրաֆիկական պատկերացմամբ, կարելի է ներկայացնել հետևյալ կերպ.

Ռուսաստանը սահման ունի բազմաթիվ պետությունների հետ: Հարավից այն սահմանակից է Ուկրաինայի, Բելառուսի, Հայաստանի, Ադրբեջանի, Կազախստանի, Չինաստանի, Մոնղոլիայի, Ճապոնիայի և մի քանի այլ երկրների հետ: Ռուսական տարածքը նաև ծածկում է մի շարք ջրային ավազաններ, որոնցից մի քանիսը՝ Հյուսիսային օվկիանոս, Կասպից ծով, Բալթիկ ծով, Սև ծով, Ձիթու ծով, նաև մի քանի այլ ավազաններ:

Թեմա՝ «Ամբողջ ցուցիչով աստիճան» թեմայի ամփոփում։

1․ Գրել բացասական ցուցիրով աստիչանի տեսքով․

a^-15 b^-10 c^-5 d^-13 e^-4

n^-6 k^-6 17^-18 15^-9 13^-14

2․ Հաշվել կոտորակի արժեքը․

1/25 1/16 1/49 1/81 1

3․ Ներկայացնել միանդամի տեսքով․

a⁴b² c³d¹² e²⁷k^-45 -m^-30n¹⁰

4k⁶p⁶ -3x^-12y⁴ 1/3a^-10z⁶ 1/2b⁹y^-12

4․ Գրել ամբողջ ցուցիչով աստիճանի տեսքով․

2⁷ 5⁷ 4⁶

7⁸ 3¹⁵ 6⁹

11⁶ 9¹⁶

5․ Գրեք ամբողջ ցուցիչով աստիճանի տեսքով․

(10/12)² (4/25)³ (25/49)⁴

(m/a)¹² (m/a)⁸ (n/a)¹²

6․ Համեմատել․

ա)>

բ)=

գ)>

դ)>

ե)>

Թեմա՝ Ամբողջ ցուցիչով աստիճան։

Եթե n-ը բնական թիվ է և a≠0, ապա a⁻ⁿ գրելով` հասկանում են a⁻ⁿ=1/aⁿ

Օրինակ

4⁻²=1/4²=1/16 9⁻¹=1/9¹=1/9

Նշենք մի նույնություն, որը գործնականում հաճախ է օգտագործվում՝

(a/b)⁻ⁿ=(b/a)ⁿ, մասնավորապես՝ (1/a)⁻ⁿ=aⁿ, a≠0

Օրինակ

1․ (2/3)⁻²=(3/2)²=9/4 2. 3⁻²=1/3²=1/9 3. (1/5)⁻³=5³=1/25

Բնական ցուցիչով աստիճանի հատկությունները տեղի ունեն նաև բացասական ամբողջ ցուցիչների դեպքում:

1. Միևնույն թվի աստիճանները բազմապատկելիս ցուցիչները գումարվում են՝ a^s⋅a^t=a^s+t

Օրինակ

a⁻³⋅a⁻⁵=a^−3+(−5)=a⁻⁸

2. Միևնույն թվի աստիճանները բաժանելիս ցուցիչները հանվում են՝ a^s:a^t=a^s−t

Օրինակ

a⁻³:a⁻⁷=a^{−3−(−7)}=a⁻³⁺⁷=a⁴

3. Աստիճանը աստիճան բարձրացնելիս ցուցիչները բազմապատկվում են՝ (a^s)t=a^s⋅t

Օրինակ

(a⁻³⁾⁻⁵=a^{−3⋅(−5)}=a¹⁵

4. Երկու թվերի արտադրյալի աստիճանը հավասար է այդ թվերի նույն աստիճանների արտադրյալին՝ (a⋅b)^s=a^s⋅b^s

Օրինակ

(a⋅b)⁻³=a⁻³⋅b⁻³

Առաջադրանքներ։
1․ Հաշվել

1 1 1 1

2․ Հաշվել․

2 1 0.5 0.25

3 1 -0.(3) 0.04

3․ Գրել ամբողջ ցուցիչով աստիճանի տեսքով․

2³ 2⁸ 9^-1 2²

3^-1 3^-4 5¹

2^-4 5^-2 1¹

9² 0.5^-1

4․ Հաշվել․

ա․ 1000,100,100,10,1,0.1,0.01,0.001,0.0001

բ․ 32,16,8,4,2,1,0.2,0.4,0.16,0.36

գ․-81,-9,-3,1,-0.3,-0.9,-0.81

5․ Հաշվել․

ա․ 1,-1,-1,-1,-1

բ․1,-1,1,1,-1

գ․0.25,-4,4,0.25,-0.25

Թեմա՝ Առանցքային և կենտրոնային համաչափություն։

Առանցքային համաչափության ժամանակ հարթության յուրաքանչյուր կետի որոշակի օրենքով համապատասխանության մեջ է դրվում հարթության մեկ այլ կետ:

Օրենքը հետևյալն է:

1. M կետից տարվում է ուղղահայաց համաչափության առանցքին (ուղղին) և ստացվում է P կետը՝ ուղղահայացի հատման կետը համաչափության առանցքի հետ:  

2. Ուղղահայացի վրա տեղադրվում է PM1=PM հատվածը և գտնվում է M1 կետը:

Այսպիսով, հարթության ցանկացած M կետի համար գտնվում է միակ՝ նրան համաչափ M1 կետը:

M և M1 կետերը կոչվում են համաչափ տրված առանցքի նկատմամբ (համաչափության առանցքի), եթե

1) MM1 հատվածը ուղղահայաց է համաչափության առանցքին,

2) համաչափության առանցքը անցնում է MM1 հատվածի միջնակետով՝  PM1=PM

Բազմանկյունները համաչափ արտապատկերելու համար բավական է արտապատկերել նրանց գագաթները և միացնել ստացված կետերը:  

Ուշադրություն

Առանցքային համաչափության ժամանակ

1. հատվածը գալիս է նույն երկարության հատվածի (կետերի միջև երկարությունները պահպանվում են),

2. ճառագայթը գալիս է ճառագայթի, ուղիղը՝ ուղղի,

3. պատկերները գալիս են հավասար պատկերների:

Երբեմն համաչափության երևույթներ հանդիպում ենք նաև բնության մեջ:

Կենտրոնական համաչափության ժամանակ M կետը արտապատկերվում է M1 կետի հետևյալ օրենքով:

1. M և O (համաչափության կենտրոն) կետերով տանում ենք ուղիղ:

2. Ուղղի վրա տեղադրում ենք OM1=OM հատվածը և գտնում ենք M1 կետը:

M և M1 կետերը կոչվում են համաչափ O կետի նկատմամբ, եթե O -ն MM1 հատվածի միջնակետն է՝  OM1=OM

Բազմանկյունները համաչափ արտապատկերելու համար բավական է արտապատկերել նրանց գագաթները և միացնել ստացված կետերը: 

Ուշադրություն

Ինչպես և առանցքային համաչափության ժամանակ, այս դեպքում ևս

1. հատվածը գալիս է նույն երկարության հատվածի (կետերի միջև երկարությունները պահպանվում են),

2. ճառագայթը գալիս է ճառագայթի, ուղիղը՝ ուղղի,

3. պատկերները գալիս են հավասար պատկերների:

Նկարում պատկերված ծառերը նույն գույնի և չափի են, սակայն ունեն մի կարևոր տարբերություն. առաջին ծառի ձախ և աջ մասերն իրար նման են, մինչդեռ երկրորդ ծառի ձախ և աջ մասերն իրարից զգալի տարբերվում են։

Բնության մեջ հաճախակի են հանդիպում համաչափության առանցք ունեցող օբյեկտներ՝ կենդանիներ, բույսեր և այլն։ Մարդիկ և կենդանիների մեծ մասն ունեն համաչափության առանցքներ։ Ոչ բոլոր կենդանիներն ունեն համաչափության առանցք, օրինակ խխունջը չունի։ Որոշ բույսեր ունեն մեկից ավելի համաչափության առանցք, օրինակ երիցուկը։ «Ամենահամաչափ» պատկերը շրջանագիծն է, այն ունի անվերջ քանակությամբ համաչափության առանցքներ՝ կենտրոնով անցնող ցանկացած ուղիղ համաչափության առանցք է։ Անմոռուկը համաչափության առանցքները 5-ն են։

Առանցքային համաչափությամբ օժտված պատկերներ։

Առաջադրանքներ։

1. O կետը AL հատվածը բաժանում է երկու հավասար մասերի: Գտնել  հատվածի միջնակետի նկատմամբ համաչափ կետեր:

AL,BK,CJ,DI,EH,FG

2. Տրված է AL հատվածը: Գտնել D կետի նկատմամբ համաչափ կետերը:

CE,BF,AG

3. Ո՞ր կետն է C կետին համաչափ՝ (0;−4) կետի նկատմամբ:

H

4. Գտնել Оx առանցքի նկատմամբ B կետին համաչափ կետը:

D,A

5․ Կոորդինատային հարթության վրա կառուցիր հետևյալ գագաթներով եռանկյունը` A(9; 3), B(3;−9) և C(−9; −3)։ Կառուցել A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> եռանկյունը, որը համաչափ է տրվածին` y=3 ուղղի նկատմամբ: Գրել  A₁B₁C₁ եռանկյան գագաթների կոորդինատները:

6․ Կոորդինատային հարթության վրա գծիր քառանկյուն, որի գագաթները հետևյալ կետերն են՝

A(18; 6), B(6; −18), C(−18; −6) և D(−6; 18)։ Գծել A₁B₁C₁D₁ քառանկյունը, որը համաչափ է տրված քառանկյանը՝ (0;0) կետի նկատմամբ: Գրել  A₁B₁C₁D₁ քառանկյան գագաթները:

7․ Նշել այն պատկերները, որոնք ունեն համաչափության կենտրոն:

• Իննանկյուն
• Սեղան
• Քառակուսի
• Ուղղանկյուն

8․ Նշել այն պատկերները, որոնք ունեն համաչափության առանցք: 

• Շրջան
• Քառանկյուն
• Եռանկյուն
• Շեղանկյուն

9․ Նշել այն տառերը և թվերը, որոնց տեսքն ունի համաչափության առանցք: