Թեմա՝ Պարզագույն իռացիոնալ անհավասարումներ։

Եթե անհավասարման անհայտը գտնվում է քառակուսի արմատի նշանի տակ, ապա  այդպիսի անհավասարումը անվանում են իռացիոնալ: 

Սովորենք լուծել պարզագույն իռացիոնալ հավասարումները: Պարզագույն իռացիոնալ անհավասարումներն են՝ √x<a և √x>a, որտեղ a -ն տրված իրական թիվ է:

Դիտարկենք √x<a անհավասարումը:

1) Եթե a≤0, ապա թվաբանական քառակուսի արմատի սահմանման համաձայն, անհավասարումը լուծում չունի:

2) Եթե a>0, ապա պետք է անհավասարումը բարձրացնել քառակուսի և պահանջել, որ արմատն իմաստ ունենա (արմատատակ թիվը լինի ոչ բացասական): Եկանք հետևյալ համակարգին՝

Որպես պատասխան ստանում ենք հետևյալ կրկնակի անհավասարումը՝ 0≤x<a²

Դիտարկենք √x>a անհավասարումը:

1) Եթե a<0, ապա ձախից ոչ բացասական թիվ է, իսկ աջից՝ բացասական: Անհավասարումը միշտ ճիշտ է, եթե արմատն իմաստ ունի:

Հետևաբար այս դեպքում անհավասարման պատասխանը ԹԱԲ -ն է՝ [0;+∞)

2) Եթե a≥0, ապա պետք է անհավասարումը բարձրացնել քառակուսի և պահանջել, որ արմատն իմաստ ունենա (արմատատակ թիվը լինի ոչ բացասական): Գալիս ենք հետևյալ համակարգին՝

Որպես պատասխան ստանում ենք հետևյալ անհավասարումը՝ x>a²

Նման ձևով վարվելով՝ կարելի է լուծել պարզագույն ոչ խիստ անհավասարումները:

√x ≤a անհավասարման դեպքում գալիս ենք հետևյալ եզրակացություններին:

1) Եթե a<0, լուծում չկա: 

2) Եթե a≥0, ապա x∈[0;a2]

√x ≥ a անհավասարման դեպքում գալիս ենք հետևյալ եզրակացություններին:

1) Եթե a<0, պատասխանը ԹԱԲ -ն է՝ [0;+∞)

2) Եթե a≥0, ապա x∈[a2;+∞)

Օրինակ

Լուծենք √2x−1<3 իռացիոնալ անհավասարումը:

1) Սկզբում գտնենք ԹԱԲ -ը՝ 2x−1≥0

2) Երկու մասերը բարձրացնենք քառակուսի՝ (√2x−1)² ≥ 3²

3) Եկանք հետևյալ համակարգին՝

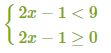
4) Լուծենք ստացված համակարգը՝

5) Պատասխանը ստացված բազմությունների հատումն է՝ x∈[0.5;5)

Առաջադրանքներ։

1․Լուծել անհավասարումները;

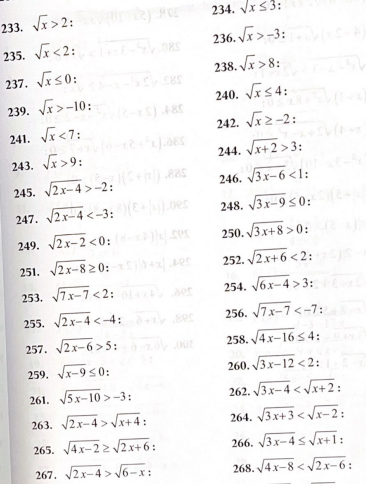
233. x ∈ (4; +∞)

234. x ∈ [0;9]

235. x ∈ [0;4)

236. x ∈ [0;+∞)

237.x=0

238.x ∈ (64;+∞)

239.x ∈ [0;+∞)

240.x ∈ [0;16)

241. x ∈ [0;49)

242.x ∈ [0;+∞)

243. x ∈ (81;+∞)

244. x ∈ (7;+∞)

245.x ∈ [2;+∞)

246. x ∈ [2;7/3)

247. Ø

248.x=3

249.Ø

250.x ∈ (-8/3;+∞)

251. x(>=)4

252.x ∈ [-3;-1]

253.x ∈ [1;11/7)

254. x ∈ (5/6;+∞)

255.Ø

256.Ø

257.x ∈ (15,5;+∞)

258.x ∈ [4;8]

259.x=9

260. x ∈ [4; 16/3)

261.x(>=)2

262.Ø

263.x ∈ [2;8)

264.Ø

265.x ∈ [4; +∞)

266. x ∈ [4/3; 2,5]

267. x ∈ (10/3; 6]

268.Ø

2․ Լուծել անհավասարումները։

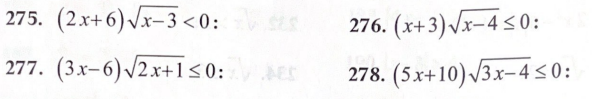
275.Ø

276.x ∈ (2; +∞)

277. x ∈ [-1/2; 2]

278.x ∈ {4/3}

Թեմա՝ Սեղանի մակերեսը։

Առաջադրանքներ։

1․ Ունենք ուղղանկյուն սեղան, որի հիմքեր են 9սմ ,18սմ, իսկ մեծ սրունքն, որն հիմքի հետ կազմում է ∠30° -ի անկյուն, հավասար է 16սմ ։ Գտնել սեղանի մակերեսը։

S=108սմ²

2․ Սեղանի հիմքերը հարաբերում են, ինչպես 2:3, միջին գիծը 10 սմ է, իսկ բարձրությունը 4 սմ: Գտնել սեղանի հիմքերը և մակերեսը:

Հիմքերը — 12սմ, 8սմ
S=40սմ²

3․ Հավասարասրուն սեղանի բութ անկյունը 135^օ է, իսկ այդ անկյան գագաթից տարված բարձրությունը մեծ հիմքը տրոհում է 1,4 սմ և 3․4 սմ հատվածների։ Գտնել սեղանի մակերեսը:

S=4,76սմ²

4․ Հավասարասրուն սեղանի մեծ հիմքը 10 մ է, բարձրությունը՝ 3 մ, իսկ սրունքի և մեծ հիմքի կազմած անկյունը՝ 45⁰: Գտեք սեղանի փոքր հիմքը և մակերեսը։

Փոքր հիմքը — 4սմ
S=21սմ²

1.Գնահատեք Ճապոնիայի բնական պայմանները՝ որպես տնտեսական զարգացման նախադրյալ:

Ճապոնիայի բնական պայմանները կարևոր դեր են խաղում երկրի տնտեսական զարգացման ձևավորման մեջ։

2. Ինչպիսի՞ն է Ճապոնիայի ռեսուրսաապահովվածությունը:

Ճապոնիայի ռեսուրսաապահովվածությունը հիմնականում համարվում է սակավ։ Երկիրը գրեթե չունի խոշոր բնական ռեսուրսներ, սակայն կարողացել է զարգանալ՝ հենվելով մարդկային ռեսուրսների, տեխնոլոգիաների և արտաքին առևտրի վրա։

3. Բնութագրե՛ք Ճապոնիայի բնակչության վերարտադրությունն ու կազմը:

Ճապոնիայի բնակչության վերարտադրությունն ու կազմը ունի մի շարք առանձնահատկություններ, որոնք ազդում են ինչպես երկրի սոցիալական, այնպես էլ տնտեսական վիճակի վրա։

4. Բնութագրե՛ք Ճապոնիայի կլիման:

Ճապոնիայի կլիման բազմազան է և ձևավորվում է նրա աշխարհագրական դիրքով, ռելիեֆով և օվկիանոսային հոսանքներով։ Ահա Ճապոնիայի կլիմայի հիմնական բնութագրերը՝

5. Նշե՛ք երկրի խոշորագույն քաղաքներն, պատմիր Տոկիոյի մասին:

Տոկիո (Tokyo) – երկրի մայրաքաղաքը և աշխարհի ամենամեծ մետրոպոլիտենային տարածքը։
Յոկոհամա (Yokohama) – խոշոր նավահանգիստ և արդյունաբերական կենտրոն։
Օսակա (Osaka) – առևտրային, արդյունաբերական և մշակութային հզոր կենտրոն։
Նագոյա (Nagoya) – մեքենաշինության, մասնավորապես ավտոմոբիլաշինության կենտրոն։
Սապորո (Sapporo) – Հոկկայդոյի գլխավոր քաղաքը՝ հայտնի ձմեռային մարզաձևերով։
Կոբե (Kobe) – խոշոր նավահանգիստ և միջազգային առևտրի կենտրոն։
Կիոտո (Kyoto) – Ճապոնիայի հնագույն մայրաքաղաքներից, մշակութային և պատմական կենտրոն։

Տոկիոն ոչ միայն Ճապոնիայի քաղաքական, տնտեսական և մշակութային կենտրոնն է, այլև համաշխարհային մեծությամբ մայրաքաղաք, որը միավորում է տեխնոլոգիական զարգացումը և դարավոր ավանդույթները։

Թեմա՝ Սեղանի մակերեսը։

Բարձրությամբ և անկյունագծով սեղանը բաժանվում է երեք եռանկյունների: Սեղանի մակերեսը հաշվում ենք, որպես այդ եռանկյունների մակերեսների գումար:

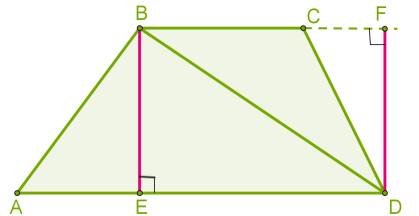
S_ABCD=S_ABD+S_DBC S_ABCD=AD⋅BE/2+BC⋅DF/2=AD⋅BE/2+BC⋅BE/2=(AD+BC)⋅BE/2

Եթե սեղանի զուգահեռ կողմերը (հիմքերը) նշանակենք a և b, իսկ բարձրությունը՝ h, ապա՝

S_սեղան=a+b/2⋅h

Ուշադրություն

Նշենք մի քանի կարևոր հետևանքներ:

1. Եթե եռանկյունների բարձրությունները հավասար են, ապա նրանց մակերեսները հարաբերվում են ինչպես հիմքերը:

2. Եթե եռանկյունների հիմքերը հավասար են, ապա նրանց մակերեսները հարաբերվում են ինչպես բարձրությունները:

3. Եթե եռանկյունների բարձրություններն ու հիմքերը հավասար են, ապա եռանկյունները հավասարամեծ են: Օրինակ՝ միջնագիծը եռանկյունը բաժանում է երկու հավասարամեծ եռանկյունների:

Առաջադրանքներ։

1․ Սեղանի հիմքերը 3 մ և 7 մ են, իսկ բարձրությունը՝ 6 մ: Հաշվիր սեղանի մակերեսը:

3+7/2×6=30

2․ Ո՞ր հատվածի երկարությունն է հավասար սեղանի հիմքերի կիսագումարին:

միջնուղղահայացի
միջին գծի
անկյունագծի

3․Գտնել AD և BC հիմքերով ABCD սեղանի մակերեսը, եթե՝

ա) AD=21 սմ, BC=17 սմ, BH բարձրությունը 7սմ է,

21+17/2×7=133սմ

բ) ∠D=30, AD=10սմ, BC=2սմ, CD=8սմ,

10+5/2x√57,75=7,5x√57,75=56,9

գ) CD⊥AD, AD=13սմ, CD=8սմ, BC=5սմ:

13+5/2x√48=9x√48=62,3

5․ ABCD սեղանի AD և BC հիմքերը համապատասխանաբար 10 սմ և 8 սմ են: ACD եռանկյան մակերեսը 30սմ² է: Գտեք սեղանի մակերեսը:

(10+8):2×6=54

6. Ուղղանկյուն սեղանի մակերեսը 30 սմ² է, պարագիծը՝ 28 սմ, իսկ փոքր սրունքը՝ 3 սմ: Գտնել սեղանի մեծ սրունքը:

Սրունքը 5սմ է։

7. Գտնել ուղղանկյուն սեղանի մակերեսը, որի փոքր կողմերը 6սմ են, իսկ մեծ անկյունը՝ 135^o:

(12+6):2=9
9×6=54
Պատ․՝54սմ²։

8․ Տրված է ուղղանկյուն սեղան, որի փոքր հիմքը 6 սմ է: Փոքր սրունքը 18 սմ է, իսկ մեծը՝ հիմքի հետ կազմում է ∡45° -ի անկյուն: Գտնել սեղանի մակերեսը:

(6+18+6):2=15
15×18=270
Պատ․՝270սմ²։

Թեմա՝ Թվաբանական քառակուսի արմատների հատկությունները։

1․ Պարզեցնել արտահայտությունը․

ա)5√2

բ)√2

գ)-4√a

դ)(a-3)√x

ե)√a

զ)-√2

2․ Համեմատել արտահայտությունների արժեքները առանց արմատը հաշվելու։

ա)>

բ)>

գ)<

դ)<

ե)<

զ)>

3․ Պարզեցնել արտահայտությունը․

ա)√3-1

բ)5-√5

գ)√3-√2

դ)4-√10

4․ Հայտարարում ազատվել արմատանշանից։

ա)√2+1

բ)√3+1/2

գ)6-2√5/4

դ)2+√3

ե) √3-√2

զ)4-√15

5․ Կրճատել կոտորակը․

ա)2/2+√2

բ)√3-3/√3

գ)1+√x

6․ Արտադրիչը տանել արմատանշանի տակ․

ա)8

բ)-12

գ)100

դ)-250

Բերեք հասարակական առաջնորդի օրինակ ձեր կյանքից

Իմ կյանքից հասարակական առաջնորդի օրինակ կարող եմ բերել մեր դպրոցի տնօրենը։ Նա ոչ միայն կազմակերպում է դպրոցի աշխատանքները, այլև միշտ ուշադրություն է դարձնում աշակերտների կարիքներին, մասնակցում է հասարակական միջոցառումների կազմակերպմանը և աջակցում է համայնքի տարբեր նախաձեռնություններին։

ներկայացրեք այն հատկանիշները, որոնց համաձայն՝ նրան ընկալում են որպես առաջնորդ։

Նրան ընկալում են որպես առաջնորդ, քանի որ նա պատասխանատու է, արդար, հաղորդակցվող, նվիրված, խնդիրներ լուծելու ունակությամբ և իր օրինակով ոգեշնչող մարդ է, ում վստահում և հարգում է համայնքը։

Որոնք են իշխանության դրական և բացասական կողմերը։ Իշխանությունը առավելություն է , արտոնություն ․ թե․․․

Իշխանության դրական կողմերն են կարգ ու կանոնի ապահովումը, տնտեսական և սոցիալական զարգացումը, արդարության և անվտանգության պահպանումը, ինչպես նաև բարեփոխումների իրականացումը։ Բացասական կողմերն են կոռուպցիայի վտանգը, անհատական ազատությունների սահմանափակումը, անարդարության ու չարաշահման հնարավորությունը, ինչպես նաև պետական ռեսուրսների անարդյունավետ կառավարումը։ Իշխանությունը և՛ առավելություն է, և՛ արտոնություն, բայց ամենից առաջ՝ մեծ պատասխանատվություն։

Ինչ միջոցներով է իշխանությունն ազդում մարդկանց վարքագծի վրա։

Իշխանությունն ազդում է մարդկանց վարքագծի վրա օրենքների և կանոնակարգերի հաստատմամբ, խրախուսումների ու պատժամիջոցների կիրառմամբ, կրթական ու տեղեկատվական քաղաքականության միջոցով, ինչպես նաև հասարակական կարծիքի ձևավորմամբ։

Ինչպես, ինչ միջոցներով է պետությունը կարգուկանոն հաստատում և պաշտպանում։

Պետությունը կարգուկանոն է հաստատում և պաշտպանում օրենքների ընդունմամբ, իրավապահ մարմինների գործունեությամբ, դատարանների միջոցով արդարադատության իրականացմամբ, կրթական ու դաստիարակչական ծրագրերով, ինչպես նաև հասարակական կարգի վերահսկման մեխանիզմներով։

Թեմա՝ Մեկ անհայտով գծային անհավասարումների համախմբեր։

Տրված են x անհայտով մի քանի անհավասարումներ և հավասարումներ։ Եթե պետք է գտնել բոլոր այն x թվերը, որոնցից յուրաքանչյուրը հանդիսանում է դրանցից մեկի լուծում, ապա ասում են, որ պետք է լուծել մեկ x անհայտով համախումբ։

Համախումբը լուծելու համար պետք է լուծել այդ համախմբի յուրաքանչյուր անհավասարումը կամ հավասարումը և այնուհետև գտնել ստացված լուծումների բազմությունների միավորումը, դա էլ հենց կհանդիսանա տվյալ համախմբի բոլոր լուծումների բազմությունը։

Օրինակ`

Լուծենք 5x – 2 < 3 և 4x + 3 > 0 համախումբը

Լուծում

5x < 5 4x > -3 կստանանք՝

x < 1 x > – 3 / 4

Պատ․՛ ( – ∞ ; 1) ∪ [ – 3/4; + ∞] = ( – ∞ ; +∞)

Այսինքն համախմբի լուծումը՝ բոլոր իրական թվերի համախումբն է՝ R – ը:

Առաջադրանքներ։

1․ 2; 3; -5 թվերից ո՞րն է հետևյալ համախմբի լուծում․

ա)2,3

բ)3, -5

գ)2,3

2․Լուծել համախումբը․

ա) x ∈ (-∞;2) ∪ (3; +∞)

բ)x ∈ (3; 5)

գ)x ∈ (-∞; -2) ∪ (3; +∞)

դ)x ∈ (-∞;2) ∪ (3; +∞)

3․ Գտնել համախմբի լուծումները․

ա)x ∈ (-∞;2)

բ) x ∈ (-∞;+∞)

գ)լուծում չունի

դ)x ∈ (-∞;+∞)

4․ Լուծել համախումբը․

ա)x ∈ (-∞;+∞)

բ)x ∈ (0;+∞)